Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T22:13:16.062Z Has data issue: false hasContentIssue false
  • English
  • Français

ON LENGTH DISTORTIONS WITH RESPECT TO QUADRATIC DIFFERENTIAL METRICS

Published online by Cambridge University Press:  22 August 2014

ZONGLIANG SUN
ZONGLIANG SUN*
Affiliation:
Department of Mathematics, Shenzhen University, Shenzhen 518060, P. R. China E-mail: moonshoter@163.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we consider the question about length distortions under quasiconformal mappings with respect to quadratic differential metrics. More precisely, let X and Y be closed Riemann surfaces with genus at least 2, and f: X → Y being a K-quasiconformal mapping. Given two quadratic differential metrics |q1| and |q2| with unit areas on X and Y respectively, whether there exists a constant 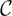$\mathcal C$ depending only on K such that 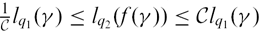$\frac{1}{\mathcal C} l_{q_1} (\gamma) \leq l_{q_2} (f(\gamma)) \leq \mathcal C l_{q_1} (\gamma)$ holds for any simple closed curve γ ⊂ X. Here lqi(α) denotes the infimum of the lengths of curves in the homotopy class of α with respect to the metric |qi|, i = 1, 2. We give positive answers to this question, including the aspects that the desired constant 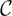${\mathcal C}$ explicitly depends on q1, q2 and K, and that the constant 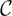$\mathcal C$ is universal for all the quantities involved.

Keywords

Primary 30F45Secondary 51M25
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 56 , Issue 3 , September 2014 , pp. 681 - 689
Copyright
Copyright © Glasgow Mathematical Journal Trust 2014 

References

REFERENCES

1.Ahlfors, L., Lectures on quasiconformal mappings (Van Nostrand Reinhold Princeton, NJ, 1966).Google Scholar
2.Duchin, M., Leininger, C. and Rafi, K., Length spectra and degeneration of flat metrics, Invent. Math. 182 (2) (2010), 231–277.CrossRefGoogle Scholar
3.Fathi, A., Laudenbach, F. and Poenaru, V., translated by D. Kim and D. Margalit, Thurston's work on surfaces (Mathematical Notes, 48, Princeton University Press, Princeton, 2012).Google Scholar
4.Gardiner, F., Teichmüller theory and quadratic differentials (John Wiley, New York, NY, 1987).Google Scholar
5.Hamenstädt, U., Closed Teichmüller geodesics in the thin part of moduli space, arXiv:math/0511349 (2009).Google Scholar
6.Imayoshi, Y. and Taniguchi, M., An introduction to Teichmüller space (translated and revised from the Japanese by the authors) (Springer-Verlag, Tokyo, Japan, 1992).Google Scholar
7.Kerckhoff, S., The asymptotic geometry of Teichmüller space, Topology 19 (1) (1980), 23–41.CrossRefGoogle Scholar
8.Kontsevich, M. and Zorich, A., Connected components of the moduli spaces of Abelian differentials with prescribed singularities, Invent. Math. 153 (3) (2003), 631–678.CrossRefGoogle Scholar
9.Strebel, K., Quadratic differentials (Springer-Verlag, New York, NY, 1984).CrossRefGoogle Scholar
10.Thurston, W., On the geometry and dynamics of diffeomorphisms of surfaces, Bull. Amer. Math. Soc. 19 (2) (1988), 417–431.Google Scholar
11.Wolpert, S., The length spectra as moduli for compact Riemann surfaces, Ann. Math. 109 (2) (1979), 323–351.CrossRefGoogle Scholar