Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-15T10:19:41.926Z Has data issue: false hasContentIssue false
  • English
  • Français

On limit problems associated with some inequalities

Published online by Cambridge University Press:  18 May 2009

P. H. Diananda
P. H. Diananda
Affiliation:
University of Singapore
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let {an} be a sequence of non-negative real numbers. Suppose that

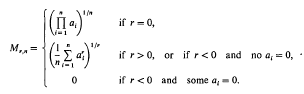
Then M1,n is the arithmetic mean, MO,n the geometric mean, and Mr,n the generalized mean of order r, of a1, a2, …, an. By a result of Everitt [1] and McLaughlin and Metcalf [5], {n(Mr,n–Ms,n)}, where r ≧ l ≧ s, is a monotonic increasing sequence. It follows that this sequence tends to a finite or an infinite limit as n → ∞. Everitt [2, 3] found a necessary and sufficient condition for the finiteness of this limit in the cases r, s = 1, 0 and r ≧ 1 > s > 0. His results are included in the following theorem.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 14 , Issue 2 , September 1973 , pp. 123 - 127
Copyright
Copyright © Glasgow Mathematical Journal Trust 1973

References

REFERENCES

1.Everitt, W. N., On an inequality for the generalized arithmetic and geometric means, Amer. Math. Monthly 70 (1963), 251–255.Google Scholar
2.Everitt, W. N., On a limit problem associated with the arithmetic–geometric mean inequality, J. London Math. Soc. 42 (1967), 712–718.CrossRefGoogle Scholar
3.Everitt, W. N., Corrigendum to [2], J. London Math. Soc. (2) 1 (1969), 428–430.CrossRefGoogle Scholar
4.Hardy, G. H., J. E. Littlewood and G. Pólya, Inequalities (Cambridge, 1934).Google Scholar
5.McLaughlin, H. W. and Metcalf, F. T., An inequality for generalized means, Pacific J. Math. 22 (1967), 303–311.CrossRefGoogle Scholar