Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-15T15:49:12.928Z Has data issue: false hasContentIssue false
  • English
  • Français

On polylogarithms

Published online by Cambridge University Press:  18 May 2009

M. S. P. Eastham
M. S. P. Eastham
Affiliation:
The UniversityReading
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The nth order polylogarithm Lin(z) is defined for |z| ≦ 1 by

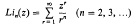
([4, p. 169], cf. [2, §1. 11 (14) and § 1. 11. 1]). The definition can be extended to all values of zin the z-plane cut along the real axis from 1 to ∝ by the formula

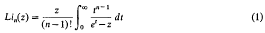
[2, §1. 11(3)]. Then Lin(z) is regular in the cut plane, and there is a differential recurrence relation [4, p. 169]

It is convenient to extend the sequence Lin(z) backwards in the manner suggested by (2) and define

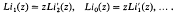
Then Li1(z)= – log(l–z), and Lin(z) is a rational function of z for n= 0, – 1, – 2,…. Formula (2) now holds for all integers n.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 6 , Issue 4 , July 1964 , pp. 169 - 171
Copyright
Copyright © Glasgow Mathematical Journal Trust 1964

References

REFERENCES

1.Bowman, F., Note on the integral J. London Math. Soc. 22 (1947), 172–173.CrossRefGoogle Scholar
2.Erdélyi, A. et al. , Higher transcendental functions, Vol. I (New York, 1953).Google Scholar
3.Glaisher, J. W. L., Relations connecting sums of powers…, Quart. J. Math. 44 (1913), 170–186.Google Scholar
4.Lewin, L., Dilogahthms and associated functions (London, 1958).Google Scholar