No CrossRef data available.
Article contents
On residually transcendental valued function fields of conics
Published online by Cambridge University Press: 18 May 2009
Extract
Let K/Kobe a finitely generated field extension of transcendence degree 1. Let u0 be a valuation of Koand v a valuation of Kextending v0such that the residue field of vis a transcendental extension ofthe residue field k0of vo/such a prolongation vwill be called a residually transcendental prolongation of v0. Byan element with the uniqueness propertyfor (K, v)/(K0, v0) (or more briefly for v/v0)we mean an element / of Khaving u-valuation 0 which satisfies (i) the image of tunder the canonicalhomomorphism from the valuation ring of vonto the residue field of v(henceforth referred to as the v-residue ot t) is transcendental over ko; that is vcoincides with the Gaussian valuation 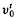 on the subfield K0(t) defined by
on the subfield K0(t) defined by 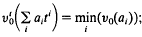 (ii) vis the only valuation of K (up to equivalence) extending the valuation
(ii) vis the only valuation of K (up to equivalence) extending the valuation 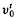 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1996

