Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-15T10:48:36.156Z Has data issue: false hasContentIssue false
  • English
  • Français

On some solutions of second order hyperbolic differential equations with constant coefficients

Published online by Cambridge University Press:  18 May 2009

J. S. Lowndes
J. S. Lowndes
Affiliation:
Department of Mathematics, University of Strathclyde, Glasgow G1 1XH
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If we seek solutions of the hyperbolic differential equation

which depend only on the variables i and , we see that these solutions must be even in r and satisfy the differential equation

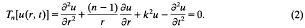
The object of this paper is to show that some recent results in the fractional calculus can be used to prove the following theorem.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 29 , Issue 1 , January 1987 , pp. 69 - 72
Copyright
Copyright © Glasgow Mathematical Journal Trust 1987

References

REFERENCES

1.Courant, R. and Hilbert, D., Methods of mathematical physics, Vol. 2 (Interscience, 1962).Google Scholar
2.Lowndes, J. S., An application of some fractional integrals, Glasgow Math. J. 20 (1979), 35–41.CrossRefGoogle Scholar
3.Magnus, W., Oberhettinger, F. and Soni, R. P., Formulas and theorems for the special functions of mathematical physics, 3rd. ed. (Springer-Verlag, 1966).CrossRefGoogle Scholar