Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T06:05:28.242Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE DIOPHANTINE EQUATION x2 + d2l + 1 = yn

Published online by Cambridge University Press:  29 March 2012

ATTILA BÉRCZES  and
ISTVÁN PINK
ATTILA BÉRCZES
Affiliation:
Institute of Mathematics, University of Debrecen, Number Theory Research Group, Hungarian Academy of Sciences and University of Debrecen, H-4010 Debrecen, P.O. Box 12, Hungary e-mail: berczesa@math.klte.hu
ISTVÁN PINK
Affiliation:
Institute of Mathematics, University of Debrecen, H-4010 Debrecen, P.O. Box 12, Hungary e-mail: pinki@math.klte.hu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let d > 0 be a squarefree integer and denote by h = h(−d) the class number of the imaginary quadratic field 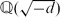. It is well known (see e.g. [25]) that for a given positive integer N there are only finitely many squarefree d's for which h(−d) = N. In [45], Saradha and Srinivasan and in [28] Le and Zhu considered the equation in the title and solved it completely under the assumption h(−d) = 1 apart from the case d ≡ 7 (mod 8) in which case y was supposed to be odd. We investigate the title equation in unknown integers (x, y, l, n) with x ≥ 1, y ≥ 1, n ≥ 3, l ≥ 0 and gcd(x, y) = 1. The purpose of this paper is to extend the above result of Saradha and Srinivasan to the case h(−d) ∈ {2, 3}.

Keywords

11D4111D61
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 54 , Issue 2 , May 2012 , pp. 415 - 428
Copyright
Copyright © Glasgow Mathematical Journal Trust 2012

References

REFERENCES

1.Arif, S. A. and Muriefah, F. S. A., on the diophantine equation x 2+2k=yn, Internat. J. Math. Math. Sci. 20 (1997), 299–304.CrossRefGoogle Scholar
2.Arif, S. A. and Muriefah, F. S. A., the diophantine equation x 2+3m=yn, Internat. J. Math. Math. Sci. 21 (1998), 619–620.CrossRefGoogle Scholar
3.Arif, S. A. and Muriefah, F. S. A., The Diophantine equation x 2+q 2k=yn, Arab. J. Sci. Eng. Sect. A Sci. 26 (2001), 53–62.Google Scholar
4.Arif, S. A. and Muriefah, F. S. A., On the Diophantine equation x 2+2k=yn II, Arab J. Math. Sci. 7 (2001), 67–71.Google Scholar
5.Arif, S. A. and Muriefah, F. S. A., On the Diophantine equation x 2+q 2k+1=yn, J. Number Theory 95 (2002), 95–100.CrossRefGoogle Scholar
6.Arno, S., Robinson, M. L. and Wheeler, F. S., Imaginary quadratic fields with small odd class number, Acta. Arith. 83 (1998), 295–330.CrossRefGoogle Scholar
7.Bennett, M. A., Ellenberg, J. S. and Ng, N. C., The Diophantine equation A 4+2dB 2=C n submitted.Google Scholar
8.Bennett, M. A. and Skinner, C. M., Ternary diophantine equations via Galois representations and modular forms, Canad. J. Math. 56 (1) (2004), 23–54.CrossRefGoogle Scholar
9.Bérczes, A., Brindza, B. and Hajdu, L., On power values of polynomials, Publ. Math. Debrecen 53 (1998), 375–381.CrossRefGoogle Scholar
10.Bérczes, A. and Pink, I., On the diophantine equation x 2+p 2k=yn, Arch. Math. 91 (2008), 505–517.CrossRefGoogle Scholar
11.Bilu, Y., Hanrot, G. and Voutier, P. M., Existence of primitive divisors of Lucas and Lehmer numbers. With an appendix by M. Mignotte, J. Reine Angew. Math. 539 (2001), 75–122.Google Scholar
12.Bosma, W., Cannon, J. and Playoust, C., The Magma algebra system. I. The user language, Computational algebra and number theory (London, 1993), J. Symbolic Comput. 24 (3–4) (1997), 235–265.CrossRefGoogle Scholar
13.Bugeaud, Y., On the diophantine equation x 2-pm=± yn, Acta. Arith. 80 (1997), 213–223.CrossRefGoogle Scholar
14.Bugeaud, Y., Mignotte, M. and Siksek, S., Classical and modular approaches to exponential and diophantine equations II. The Lebesque-Nagell equation, Compos. Math. 142 (1) (2006), 31–62.CrossRefGoogle Scholar
15.Bugeaud, Y. and Abu Muriefah, F. S., The Diophantine equation x 2+c=yn: a brief overview, Rev. Colombiana Mat. 40 (2006), 31–37.Google Scholar
16.Cangül, I. N., Demirci, M., Soydan, G. and Tzanakis, N., On the Diophantine equation x 2 + 5a11b = yn, Funct. Approx. Comment. Math. (2010), to appear.Google Scholar
17.Cangül, N., Demirci, M., Luca, F., Pintér, Á. and Soydan, G., On the Diophantine equation x 2 + 2a11b = yn, Fibonacci Quart. 48 (2010), 39–46.Google Scholar
18.Cohn, J. H. E., The diophantine equation x 2+2k=yn. II., Internat J. Math. Math. Sci., 22 (1999), 459–462.CrossRefGoogle Scholar
19.Cohn, J. H. E., The diophantine equation x 2+2k=yn, Arch. Math (Basel) 59 (1992), 341–344.CrossRefGoogle Scholar
20.Cohn, J. H. E., The diophantine equation x 2+C=yn, Acta. Arith. 65 (1993), 367–381.CrossRefGoogle Scholar
21.Cohn, J. H. E., The diophantine equation x 2+C=yn II., Acta. Arith. 109 (2003), 205–206.CrossRefGoogle Scholar
22.Ellenberg, J. S., Galois representations to ℚ-curves and the generalized Fermat Equation A 4+B 2=C p, Amer. J. Math. 126 (4) (2004), 763–787.CrossRefGoogle Scholar
23.Goins, E., Luca, F. and Togbe, A., On the Diophantine Equation x 2 + 2α5β13γ = yn, ANTS VIII Proceedings: van der Poorten, A. J. and Stein, A. (eds.), ANTS VIII, Lecture Notes in Computer Science 5011 (2008), 430–442.CrossRefGoogle Scholar
24.Győry, K., Pink, I. and Pintér, Á., Power values of polynomials and binomial Thue-Mahler equations, Publ. Math. Debrecen 65 (2004), 341–362.CrossRefGoogle Scholar
25.Heilbronn, H., On the class number in imaginary quadratic fields, Quart. J. Math. Oxford Ser. 25 (1934), 150–160.CrossRefGoogle Scholar
26.Le, M., On Cohn's conjecture concerning the diophantine equation x 2+2m=y n, Arch. Math. Basel 78 (1) (2002), 26–35.CrossRefGoogle Scholar
27.Le, M., On the diophantine equation x 2+p 2=y n, Publ. Math. Debrecen 63 (2003), 27–78.CrossRefGoogle Scholar
28.Le, M. and Zhu, H., On some generalized Lebesque-Nagell equations, J. N. Th. 131 (3) (2011), 458–469.Google Scholar
29.Lebesque, V. A., Sur l'impossibilité en nombres entierde l'equation x m=y 2+1, Nouvelle Annales des Mathématiques 9 (1) (1850), 178–181.Google Scholar
30.Ljunggren, W., Über einige arcustangensgleichungen die auf interessante unbestimmte gleichungen führen, Ark. Mat. Astr. Fys. 29A (1943), 13.Google Scholar
31.Ljunggren, W., On the diophantine equation Cx 2+D=y n, Pacific J. Math. 14 (1964), 585–596.CrossRefGoogle Scholar
32.Luca, F., On a diophantine equation, Bull. Austral. Math. Soc. 61 (2000), 241–246.CrossRefGoogle Scholar
33.Luca, F., On the equation x 2+2a3b=y n, Int. J. Math. Sci. 29 (2002), 239–244.CrossRefGoogle Scholar
34.Luca, F. and Togbe, A., On the diophantine equation x 2 + 72k =y n, Fibonacci Quart. 54 (4) (2007), 322–326.Google Scholar
35.Luca, F. and Togbe, A., On the diophantine equation x 2 + 2a5b = y n, Int. J. Number Th. 4 (6) (2008), 973–979.CrossRefGoogle Scholar
36.Luca, F., Sz. Tengely and A. Togbe, On the Diophantine Equation x 2 + C = 4y n, Ann. Sci. Math. Qübec 33 (2) (2009), 171–184.Google Scholar
37.Mignotte, M. and de Weger, B. M. M, On the equations x 2+74=y 5 and x 2+86=y 5, Glasgow Math. J. 38 (1) (1996), 77–85.CrossRefGoogle Scholar
38.Muriefah, F. S. A., On the Diophantine equation x 2+52k=y n, Demonstratio Math. 319 (2) (2006), 285–289.Google Scholar
39.Muriefah, F. S. A., Luca, F. and Togbe, A., On the diophantine equation x 2+5a13b=y n, Glasgow Math. J. 50 (2008), 175–181.Google Scholar
40.Nagell, T., Sur l'impossibilité de quelques équations a deux indeterminées, Norsk. Mat. Forensings Skifter 13 (1923), 65–82.Google Scholar
41.Nagell, T., Contributions to the theory of a category of diophantine equations of the second degree with two unknowns, Nova Acta Reg. Soc. Upsal. IV 16, Uppsala (1955), 1–38.Google Scholar
42.Pink, I., On the diophantine equation x 2+2α3β5γ7δ=y n, Publ. Math. Debrecen 70 (1–2) (2007), 149–166.CrossRefGoogle Scholar
43.Pink, I. and Rábai, Zs., On the diophantine equation x 2+5k17l=y n, Commun. Math 19 (2011), 1–9.Google Scholar
44.Ribenboim, P., Classical Theory of Algebraic Numbers (Springer, New York, 2001), 636.CrossRefGoogle Scholar
45.Saradha, N. and Srinivasan, A., Solutions of some generalized Ramanujan-Nagell equations, Indag. Math. (N.S.) 17 (1) (2006), 103–114.CrossRefGoogle Scholar
46.Saradha, N. and Srinivasan, A., Solutions of some generalized Ramanujan-Nagell equations via binary quadratic forms, Publ. Math. Debrecen 71 (3–4) (2007), 349–374.CrossRefGoogle Scholar
47.Schinzel, A. and Tijdeman, R., On the equation y m=P(x), Acta. Arith. 31 (1976), 199–204.CrossRefGoogle Scholar
48.Shorey, T. N., van der Poorten, A. J., Tijdeman, R. and Schinzel, A., Applications of the Gel'fond-Baker method to diophantine equations, in Transcendence Theory: Advances and Applications (Academic Press, London-New York, San Francisco, 1977), 59–77.Google Scholar
49.Shorey, T. N. and Tijdeman, R., Exponential Diophantine equations, Cambridge Tracts in Mathematics, 87. (Cambridge University Press, Cambridge, UK, 1986) x+240 pp.CrossRefGoogle Scholar
50.Tengely, Sz., On the diophantine equation x 2+a 2=2y p, Indag. Math. (N.S.) 15 (2004), 291–304.CrossRefGoogle Scholar
51.Tengely, Sz., On the Diophantine equation x 2+q 2m=2y p, Acta Arith. 127 (2007), 71–86.CrossRefGoogle Scholar
52.Tengely, Sz., On the Diophantine Equation x 2+C=2y n, Int. J. N. Th. 5 (6) (2009), 1117–1128.Google Scholar
53.Voutier, P. M., Primitive divisors of Lucas and Lehmer sequences, Math. Comp. 64 (1995), 869–888.CrossRefGoogle Scholar
54.Zhu, H., A note on the Diophantine equation x 2+q m=y 3, Acta. Arith. 146 (2) (2011), 195–202.CrossRefGoogle Scholar