Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-15T13:47:03.424Z Has data issue: false hasContentIssue false
  • English
  • Français

On the divisibility of r2(n)

Published online by Cambridge University Press:  18 May 2009

E. J. Scourfield
E. J. Scourfield
Affiliation:
Department of Mathematics, Westfield College, London NW3 7ST
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

During the past few years, some papers of P. Deligne and J.-P. Serre (see [2], [9], [10] and other references cited there) have included an investigation of certain properties of coefficients of modular forms, and in particular Serre [10] (see also [11]) obtained the divisibility property (1) below. Let

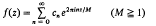
be a modular form of integral weight k ≧ 1 on a congruence subgroup of SL2(Z), and suppose that each cn belongs to the ring RK of integers of an algebraic number field K finite over Q. For c ∈ RK and m ≧ 1 an integer, write c ≡ 0 (mod m) if c ∈ m RK and c ≢ 0 (mod m) otherwise. Then Serre showed that there exists α > 0 such that

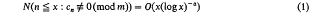
as x → ∞, where throughout this note N(n ≦ x: P) denotes the number of positive integers n ≦ x with the property P.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 18 , Issue 1 , January 1977 , pp. 109 - 111
Copyright
Copyright © Glasgow Mathematical Journal Trust 1977

References

REFERENCES

1.Delange, H., Généralisation du théoréme de Ikehara, Ann. Sci. École Norm. Sup. (3) 71 (1954), 213–242.CrossRefGoogle Scholar
2.Deligne, P. and Serre, J.-P., Formes modulaires de poids 1, Ann. Sci. École Norm. Sup. (4) 7 (1974), 507–530.CrossRefGoogle Scholar
3.Narkiewicz, W., Divisibility properties of a class of multiplicative, functions, Colloq. Math. 18 (1967), 219–232.CrossRefGoogle Scholar
4.Narkiewicz, W., Divisibility properties of some multiplicative functions, Number Theory (Colloq. Math. Soc. János Bolyai 2, Debrecen, 1968) (North-Holland, 1970), 147–159.Google Scholar
5.Rankin, R. A., The divisibility of divisor functions, Proc. Glasgow Math. Assoc. 5 (1961), 35–40.CrossRefGoogle Scholar
6.Scourfield, E. J., On the divisibility of σv(n), Acta Arith. 10 (1964), 245–285.CrossRefGoogle Scholar
7.Scourfield, E. J., On the divisibility of a modified divisor function, Proc. London Math. Soc. (3) 21 (1970), 145–159.CrossRefGoogle Scholar
8.Scourfield, E. J., Non-divisibility of some multiplicative functions, Acta Arith. 22 (1973), 287–314.CrossRefGoogle Scholar
9.Serre, J.-P., Congruences et formes modulaires, Séminaire Bourbaki (1971/72) exposé 416, Lecture Notes in Mathematics 317 (Springer-Verlag, 1973), 319–338.Google Scholar
10.Serre, J.-P., Divisibilité des coefficients des formes modulaires de poids entier, C.R. Acad. Sc. Paris Sér. A 279 (1974), 679–682.Google Scholar
11.Serre, J.-P., Divisibilité de certaines fonctions arithmétiques, Séminaire Delange-Pisot-Poitou (Théorie des nombres), 16e anneé (1974/1975) exposé 20, 28p.Google Scholar
12.Watson, G. N., Über Ramanujansche Kongruenzeigenschaften der Zerfällungsanzahlen (I), Math. Z. 39 (1935), 712–731.CrossRefGoogle Scholar