Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T06:06:50.544Z Has data issue: false hasContentIssue false
  • English
  • Français

On the generators of elementary subgroups of general linear groups

Published online by Cambridge University Press:  18 May 2009

A. W. Mason
A. W. Mason
Affiliation:
Department of Mathematics, University of Glasgow, Glasgow G12 8QW, Scotland e-mail: awm@MATHS.GLA.AC.UK.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be a ring with identity and let Eij ∈ Mn(R) be the usual n X n matrix units, where n ≥ 2 and 1≤i, j≤N. Let En(R) be the subgroup of GLn(R) generated by all Tij(q where r ∈ R and i ≄ j. For each (two-sided) R-ideal q let En(R, q) be the normal subgroup of En(R) generated by Tij(q), where q ∈ q. The subgroup En(R, q) plays an important role in the theory of GLn(R). For example, Vaserˇstein has proved that, for a larger class of rings 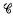(which includes all commutative rings), every subgroup S of GLn(R), when R ∈ 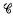and n≥3, contains the subgroup En(R, q0), where q0 is the R-ideal generated by αij, rαij-αjjr (i ≄ j, r ∈ R), for all (αij) ∈ S. (See [13, Theorem 1].) In addition Vaseršstein has shown that, for the same class of rings, En(R, q) has a simple set of generators when n ≥ 3. Let Ên(R, q) be the subgroup of En(R, q) generated by Tij(r)Tij(q)Tij(−r), where r ∈ R, q ∈ q. Then Ên(R, q) = En(R, q), for all q, when R ∈ 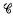and n ≥ 3.(See [13, Lemma 8].)

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 38 , Issue 1 , January 1996 , pp. 1 - 10
Copyright
Copyright © Glasgow Mathematical Journal Trust 1996

References

REFERENCES

1.Bass, H., Algebraic K-theory (Benjamin, 1968).Google Scholar
2.Bass, H., Milnor, J. and Serre, J.P., Solution of the congruence subgroup problem for SL n (n ≥ 3) and Sp 2n (n ≥ 2), Publ. Math. Inst. Hautes ÉEtud. Sci. 33 (1967), 59–137.CrossRefGoogle Scholar
3.Cohn, P. M., On the structure of the GL 2, of a ring, Publ. Math. Inst. Hautes Étud. Sci. 30 (1966), 5–53.Google Scholar
4.Dennis, R. K., The GE 2-property of discrete subrings of C, Proc. Amer. Math. Soc. 50 (1975), 77–82.Google Scholar
5.Fine, B., Algebraic Theory of the Bianchi groups (Marcel Dekker, 1989).Google Scholar
6.Karrass, A. and Solitar, D., The subgroups of a free product of two groups with an amalgamated subgroup, Trans. Amer. Math. Soc. 150 (1970), 227–255.CrossRefGoogle Scholar
7.Liehl, B., On the groups SL 2 over orders of arithmetic type, J. Reine Angew. Math. 323 (1981), 153–171.Google Scholar
8.Lyndon, R. C. and Schupp, P. E., Combinatorial Group Theory (Springer-Verlag, 1977).Google Scholar
9.Mason, A. W., Congruence hulls in SL n, J. Pure Appl. Algebra. 89 (1993) 255–272.CrossRefGoogle Scholar
10.Menal, P. and Vaserstein, L. N., On the structure of GL 2 over stable range one rings, J. Pure Appl. Algebra 64 (1990), 149–162.CrossRefGoogle Scholar
11.Newman, M., Integral Matrices (Academic Press, 1972).Google Scholar
12.Rankin, R. A., Subgroups of the modular group generated by parabolic elements of constant amplitude, Ada Arith. 18 (1971), 145–151.Google Scholar
13.Vaserstein, L. N., On the normal subgroups of GL n over a ring, Lecture Notes in Mathematics 854 (Springer-Verlag, 1981), 456–465.Google Scholar
14.Wohlfahrt, K., An extension of F. Klein's level concept, Illinois J. Math. 8 (1964), 529–535.CrossRefGoogle Scholar