Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Georgiou, Nikos
and
Guilfoyle, Brendan
2010.
A characterization of Weingarten surfaces in hyperbolic 3-space.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 80,
Issue. 2,
p.
233.
Georgiou, Nikos
and
Guilfoyle, Brendan
2010.
On the Space of Oriented Geodesics of Hyperbolic 3-Space.
Rocky Mountain Journal of Mathematics,
Vol. 40,
Issue. 4,
Alekseevsky, Dmitri V.
Guilfoyle, Brendan
and
Klingenberg, Wilhelm
2011.
On the geometry of spaces of oriented geodesics.
Annals of Global Analysis and Geometry,
Vol. 40,
Issue. 4,
p.
389.
Honda, Atsufumi
2012.
Isometric immersions of the hyperbolic plane into the hyperbolic space.
Tohoku Mathematical Journal,
Vol. 64,
Issue. 2,
Georgiou, Nikos
and
Guilfoyle, Brendan
2014.
Marginally trapped surfaces in spaces of oriented geodesics.
Journal of Geometry and Physics,
Vol. 82,
Issue. ,
p.
1.
Georgiou, Nikos
2015.
On minimal Lagrangian surfaces in the product of Riemannian two manifolds.
Tohoku Mathematical Journal,
Vol. 67,
Issue. 1,
Godoy, Yamile
and
Salvai, Marcos
2015.
Global smooth geodesic foliations of the hyperbolic space.
Mathematische Zeitschrift,
Vol. 281,
Issue. 1-2,
p.
43.
Georgiou, Nikos
and
Lobos, Guillermo A.
2016.
On Hamiltonian minimal submanifolds in the space of oriented geodesics in real space forms.
Archiv der Mathematik,
Vol. 106,
Issue. 3,
p.
285.
Georgiou, Nikos
2020.
A para-Kähler structure in the space of oriented geodesics in a real space form.
Journal of Geometry,
Vol. 111,
Issue. 3,
Georgiou, Nikos
and
Guilfoyle, Brendan
2022.
Almost paracomplex structures on 4-manifolds.
Differential Geometry and its Applications,
Vol. 82,
Issue. ,
p.
101890.
El Emam, Christian
and
Seppi, Andrea
2022.
On the Gauss map of equivariant immersions in hyperbolic space.
Journal of Topology,
Vol. 15,
Issue. 1,
p.
238.
Anarella, Mateo
and
Salvai, Marcos
2022.
Infinitesimally Helicoidal Motions with Fixed Pitch of Oriented Geodesics of a Space Form.
Acta Applicandae Mathematicae,
Vol. 179,
Issue. 1,
Godoy, Yamile
Harrison, Michael
and
Salvai, Marcos
2024.
Outer billiards in the spaces of oriented geodesics of the three‐dimensional space forms.
Journal of the London Mathematical Society,
Vol. 109,
Issue. 6,
ANDO, Naoya
2025.
Sections of time-like twistor spaces with light-like or zero covariant derivatives.
Journal of the Mathematical Society of Japan,
Vol. 77,
Issue. 3,

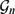 of oriented geodesics of
of oriented geodesics of 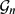 and
and 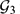 is Kähler and find an orthogonal almost complex structure on
is Kähler and find an orthogonal almost complex structure on 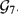 .
.