Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-15T03:26:15.874Z Has data issue: false hasContentIssue false
  • English
  • Français

On the joint spectra of doubly commuting n-tuples of semi-normal operators

Published online by Cambridge University Press:  18 May 2009

Muneo Chō  and
A. T. Dash
Muneo Chō
Affiliation:
Joetsu University of Education, Department of Mathematics, Joeisu 943, Japan
A. T. Dash
Affiliation:
Department of Mathematics and Statistics, University of Guelph, Guelph, Ontario, Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let H be a complex Hilbert space. For any operator (bounded linear transformation) T on H, we denote the spectrum of T by σ(T). Let T = (T1, …, Tn) be an n-tuple of commuting operators on H. Let Sp(T) be the Taylor joint spectrum of T. We refer the reader to [8] for the definition of Sp(T). A point v = (v1, …, vn) of ℂn is in the joint approximate point spectrum σπ(T) of T if there exists a sequence {xk} of unit vectors in H such that

.

A point v = (v1, …, vn) of ℂn is in the joint approximate compression spectrum σs(T) of T if there exists a sequence {xk} of unit vectors in H such that

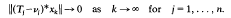
A point v=(v1, …, vn) of ℂn is in the joint point spectrum σp(T) of T if there exists a non-zero vector x in H such that (Ti-vi)x = 0 for all i, 1 ≤ j ≤ n.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 26 , Issue 1 , January 1985 , pp. 47 - 50
Copyright
Copyright © Glasgow Mathematical Journal Trust 1985

References

REFERENCES

1.Berberian, S. K., Approximate proper vectors, Proc. Amer. Math. Soc. 13 (1962, 111–114).CrossRefGoogle Scholar
2.Choi, M. D. and Davis, C., The spectral mapping theorem for joint approximate point spectrum, Bull. Amer. Math. Soc. 80 (1974), 317–321.CrossRefGoogle Scholar
3.Curto, R. E., Fredholm and invertible n-tuples of operators. The deformation problem, Trans. Amer. Math. Soc. 266 (1981), 129–159.Google Scholar
4.Dash, A. T., Joint spectra, Studia Math. 45 (1973), 225–237.CrossRefGoogle Scholar
5.Dash, A. T., A note on joint approximate point spectrum, Mimeographed lecture notes, University of Guelph and Indiana University, 1972.Google Scholar
6.Putnam, C. R., On the spectra of semi-normal operators, Trans. Amer. Math. Soc. 119 (1965), 509–523.CrossRefGoogle Scholar
7.Putnam, C. R., Commutation properties of Hilbert space operators and related topics (Springer, 1967).CrossRefGoogle Scholar
8.Taylor, J. L., A joint spectrum for several commuting operators, J. Func. Anal. 6 (1970), 172–191.CrossRefGoogle Scholar