No CrossRef data available.
Article contents
On the Jones polynomial modulo primes
Part of:
Low-dimensional topology
Published online by Cambridge University Press: 15 August 2023
Abstract
We derive an upper bound on the density of Jones polynomials of knots modulo a prime number 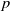 $p$, within a sufficiently large degree range:
$p$, within a sufficiently large degree range: 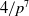 $4/p^7$. As an application, we classify knot Jones polynomials modulo two of span up to eight.
$4/p^7$. As an application, we classify knot Jones polynomials modulo two of span up to eight.
Keywords
MSC classification
Secondary:
57M27: Invariants of knots and 3-manifolds
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust
References
Birman, J. S. and Lin, X.-S., Knot polynomials and Vassiliev’s invariants, Invent. Math. 111(2) (1993), 225–270.Google Scholar
Eliahou, S. and Fromentin, J., A remarkable 20-crossing tangle, J. Knot Theory Ramif. 26(14) (2017), 1750091.Google Scholar
Ganzell, S., Local moves and restrictions on the Jones polynomial, J. Knot Theory Ramif. 23(2) (2014), 1450011.Google Scholar
Jones, V. F. R., A polynomial invariant for knots via von Neumann algebras, Bull. Am. Math. Soc. (N.S.) 12(1) (1985), 103–111.Google Scholar
Livingston, C. and Moore, A. H., KnotInfo: Table of Knot Invariants. Available at https://knotinfo.math.indiana.edu (accessed 13 April 2022).Google Scholar
Przytycki, J. H., 3-coloring and other elementary invariants of knots. In Knot Theory (Warsaw, 1995), Banach Center Publications, vol. 42 (Polish Academy of Sciences, Institute of Mathematics, Warsaw, 1998), 275–295.Google Scholar
Rolfsen, D., Knots and Links, Mathematics Lecture Series, vol. 7 (Publish or Perish, Inc., Berkeley, CA, 1976).Google Scholar


