Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T06:24:18.252Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE STANLEY DEPTH AND SIZE OF MONOMIAL IDEALS

Part of: Theory of modules and ideals Algebraic combinatorics

Published online by Cambridge University Press:  14 March 2017

S. A. SEYED FAKHARI
S. A. SEYED FAKHARI*
Affiliation:
School of Mathematics, Statistics and Computer Science, College of Science, University of Tehran, Tehran, Iran, and School of Mathematics, Institute for Research in Fundamental Sciences (IPM), P.O. Box 19395-5746, Tehran, Iran e-mail: fakhari@khayam.ut.ac.ir
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 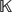$\mathbb{K}$ be a field and S = 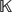${\mathbb{K}}$[x1, . . ., xn] be the polynomial ring in n variables over the field 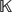$\mathbb{K}$. For every monomial ideal I ⊂ S, we provide a recursive formula to determine a lower bound for the Stanley depth of S/I. We use this formula to prove the inequality sdepth(S/I) ≥ size(I) for a particular class of monomial ideals.

MSC classification

Primary: 13C15: Dimension theory, depth, related rings (catenary, etc.)
Secondary: 05E40: Combinatorial aspects of commutative algebra 13C13: Other special types
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 59 , Issue 3 , September 2017 , pp. 705 - 715
Copyright
Copyright © Glasgow Mathematical Journal Trust 2017 

References

REFERENCES

1. Duval, A. M., Goeckner, B., Klivans, C. J. and Martin, J. L., A non-partitionable Cohen-Macaulay simplicial complex, Adv. Math. 299 (2016), 381–395.Google Scholar
2. Herzog, J., A survey on Stanley depth, in Monomial ideals, computations and applications, Proceedings of MONICA 2011, Lecture Notes in Math., vol. 2083 (Bigatti, A., Giménez, P. and Sáenz-de-Cabezón, E., Editors) (Springer, Heidelberg, 2013) 3–45.CrossRefGoogle Scholar
3. Herzog, J. and Hibi, T., Monomial ideals. Graduate Texts in Mathematics, 260. (Springer-Verlag, London, 2011).Google Scholar
4. Herzog, J., Popescu, D. and Vladoiu, M., Stanley depth and size of a monomial ideal, Proc. Amer. Math. Soc. 140 (2) (2012), 493–504.CrossRefGoogle Scholar
5. Ichim, B., Katthän, L. and Moyano-Fernández, J. J., The behavior of Stanley depth under polarization, J. Combin. Theory Ser. A 135 (2015), 332–347.CrossRefGoogle Scholar
6. Lyubeznik, G., On the arithmetical rank of monomial ideals, J. Algebra 112 (1) (1988), 86–89.CrossRefGoogle Scholar
7. Popescu, A., Special Stanley decompositions, Bull. Math. Soc. Sci. Math. Roumanie (N.S.) 53 (101) (2010), 361–373.Google Scholar
8. Popescu, D., The Stanley conjecture on intersections of four monomial prime ideals, Comm. Algebra 41 (11) (2013), 4351–4362.Google Scholar
9. Pournaki, M. R., Seyed Fakhari, S. A., Tousi, M. and Yassemi, S., What is . . . Stanley depth? Notices Amer. Math. Soc. 56 (9) (2009), 1106–1108.Google Scholar
10. Rauf, A., Stanley decompositions, pretty clean filtrations and reductions modulo regular elements, Bull. Math. Soc. Sci. Math. Roumanie (N.S.) 50 (98)(4) (2007), 347–354.Google Scholar
11. Stanley, R. P., Linear Diophantine equations and local cohomology, Invent. Math. 68 (2) (1982), 175–193.CrossRefGoogle Scholar
12. Tang, Z., Stanley depths of certain Stanley–Reisner rings, J. Algebra. 409 (2014), 430–443.Google Scholar