Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Divaani-Aazar, Kamran
Faridian, Hossein
and
Tousi, Massoud
2018.
Local homology, Koszul homology and Serre classes.
Rocky Mountain Journal of Mathematics,
Vol. 48,
Issue. 6,
Shen, Jingwen
Zhang, Pinger
and
Yang, Xiaoyan
2023.
Coartinianess of local homology modules for ideals of small dimension.
Journal of Algebra and Its Applications,
Vol. 22,
Issue. 10,


 is an ideal of
is an ideal of 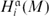 =0 for all
=0 for all 