Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-15T15:34:10.881Z Has data issue: false hasContentIssue false
  • English
  • Français

On weak approximation and convexification in weighted spaces of vector-valued continuous functions

Published online by Cambridge University Press:  18 May 2009

Marek Nawrocki
Marek Nawrocki
Affiliation:
Institute of Mathematics, A. Mickiewicz University, Matejki 48/49, 60–769 Poznan, Poland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a completely regular Hausdorff space. A Nachbin family of weights is a set V of upper-semicontinuous positive functions on X such that if u, υ ∈ V then there exists w ∈ V and t > 0 so that u, υ ≤ tw. For any Hausdorff topological vector space E, the weighted space CV0(X, E) is the space of all E-valued continuous functions f on X such that υf vanishes at infinity for all υ ∈ V. CV0(X, E) is equipped with the weighted topologywv = wv(X, E) which has as a base of neighbourhoods of zero the family of all sets of the form

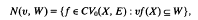
where υ ∈ Vand W is a neighbourhood of zero in E. If E is the scalar field, then the space CV0(X, E) is denoted by CV0(X). The reader is referred to [4, 6, 8] for information on weighted spaces.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 31 , Issue 1 , January 1989 , pp. 59 - 64
Copyright
Copyright © Glasgow Mathematical Journal Trust 1989

References

1.Gillman, L. and Jerison, M., Rings of continuous functions, (Van Nostrand, 1960).CrossRefGoogle Scholar
2.Kalton, N. J., Isomorphisms between spaces of vector-valued continuous functions, Proc. Edinburgh Math. Soc. 26 (1983), 29–48.CrossRefGoogle Scholar
3.Katsaras, A. K., On the strict topology in non-locally convex setting, Math. Nachr. 102 (1981), 321–329.CrossRefGoogle Scholar
4.Khan, L. A., On approximation in weighted spaces of continuous vector-valued functions, Glasgow Math. J. 29 (1987), 65–68.CrossRefGoogle Scholar
5.Klee, V., Leray-Schauder theory without local convexity, Math. Ann. 141 (1960), 286–296.CrossRefGoogle Scholar
6.Nachbin, L., Elements of approximation theory, (Van Nostrand, 1967).Google Scholar
7.Nawrocki, M., Strict dual of C b(X, E), Studio Math. 82 (1985), 33–38.CrossRefGoogle Scholar
8.Prolla, J. B., Approximation of vector-valued functions, Mathematics Studies No. 25 (North-Holland, 1977).Google Scholar
9.Schuchat, A. H., Approximation of vector-valued continuous functions, Proc. Amer. Math. Soc. 31 (1972), 97–103.CrossRefGoogle Scholar