Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-15T19:23:28.233Z Has data issue: false hasContentIssue false
  • English
  • Français

On well-bounded operators of class Г

Published online by Cambridge University Press:  18 May 2009

Adnan A. S. Jibril
Adnan A. S. Jibril
Affiliation:
Yarmouk University, Irbid-Jordan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let T be a linear operator acting in a Banach space X. It has been shown by Smart [5] and Ringrose [3] that, if X is reflexive, then T is well-bounded if and only if it may be expressed in the form

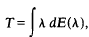
where {E(λ)} is a suitable family of projections in X and the integral exists as the strong limit of Riemann sums.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 24 , Issue 1 , January 1983 , pp. 1 - 5
Copyright
Copyright © Glasgow Mathematical Journal Trust 1983

References

REFERENCES

1.Dowson, H. R., Spectral theory of linear operators (Academic Press, London, 1978).Google Scholar
2.Dunford, N. and Schwartz, J. T., Linear operators, part I, (Wiley-Interscience, 1958).Google Scholar
3.Ringrose, J. R., On well-bounded operators. J. Austral. Math. Soc. 1 (1960), 334–343.Google Scholar
4.Ringrose, J. R., On well-bounded operators, II. Proc. London Math. Soc. (3) 13 (1963), 613–638.Google Scholar
5.Smart, D. R., Conditionally convergent spectral expansions. J. Austral. Math. Soc. 1 (1960) 319–333.Google Scholar
6.Turner, J. K., On well-bounded and decomposable operators. Proc. London Math. Soc. (3) 37 (1978), 521–544.Google Scholar