Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-15T10:32:54.832Z Has data issue: false hasContentIssue false
  • English
  • Français

Order and Schwartz distributions†

Published online by Cambridge University Press:  18 May 2009

W. A. Feldman  and
J. F. Porter
W. A. Feldman
Affiliation:
Department of Mathematics, University of Arkansas Fayetteville, Arkansas 72701, U.S.A.
J. F. Porter
Affiliation:
Department of Mathematics, University of Arkansas Fayetteville, Arkansas 72701, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The space 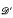of Schwartz distributions on the unit circle Г in the plane is topologically a considerable generalization of the space 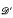of regular, finite Borel measures on Г. However, the order structure of 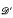is usually taken to be the same as that of 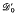: there are no “positive” distributions which are not measures. This perhaps warrants consideration, since the order structure of 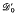generates its topology. In this paper we construct a system of order structures for 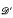which is a more natural complement in the intermediate stages to the topology of 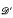and which provides an interpretation of 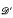with its Schwartz topology as a quotient of a generalized base norm space V′. Where 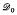denotes the space of continuous functions on Г with its supremum norm topology, V′ is the dual of 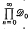. The space 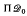contains the infinitely differentiable functions on Г with their usual topology, and (via the pointwise ordering on 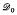) 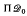in its product ordering is realized as a generalized order unit space. Some consequences for harmonic functions are discussed.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 18 , Issue 1 , January 1977 , pp. 25 - 33
Copyright
Copyright © Glasgow Mathematical Journal Trust 1977

References

REFERENCES

1.Duren, P. L., Theory of Hp-spaces (Academic Press, 1970).Google Scholar
2.Feldman, W. A. and Porter, J. F., Compact convergence and the order bidual for C(X), Pacific J. Math. 57 (1975), 113–124.CrossRefGoogle Scholar
3.Feldman, W. A. and Porter, J. F., Order units generalized for convex spaces and a Kakutanitype representation (Preprint).Google Scholar
4.Feldman, W. A. and Porter, J. F., Semibase spaces and their duality with semiorder-unit spaces (Preprint).Google Scholar
5.Jameson, G., Ordered linear spaces, Lecture Notes in Mathematics No. 141 (Springer-Verlag, 1970).CrossRefGoogle Scholar
6.Johnson, G. Jr, Harmonic functions on the unit disc I, Illinois J. Math. 12 (1968), 366–385.Google Scholar
7.Johnson, G. Jr, Harmonic functions on the unit disc II, Illinois J. Math. 12 (1968), 386–396.Google Scholar
8.Luxemburg, W. A. J. and Zaanen, A. A., Riesz spaces, Vol. I (North-Holland, 1971).Google Scholar
9.Peressini, A. L., Ordered topological vector spaces (Harper and Row, 1967).Google Scholar
10.Schwartz, L., Théorie des distributions, Actualitès Sci. Indust., Nos. 1245 (1957) and 1122 (1957).Google Scholar