Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-14T22:25:01.700Z Has data issue: false hasContentIssue false
  • English
  • Français

The Packing of Spheres in the Space lp

Published online by Cambridge University Press:  18 May 2009

Jane A. C. Burlak ,
R. A. Rankin  and
A. P. Robertson
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A point x in the real or complex space lpis an infinite sequence,(x1, x2, x3,…) of real or complex numbers such that 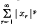is convergent. Here p ≥ 1 and we write

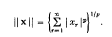
The unit sphere S consists of all points x ε lp for which ¶ x ¶ ≤ 1. The sphere of radius a≥ ≤ 0 and centre y is denoted by Sa(y) and consists of all points x ε lp such that ¶ x - y ¶ ≤ a. The sphere Sa(y) is contained in S if and only if ¶ y ¶≤1 - a, and the two spheres Sa(y) and Sa(z) do not overlap if and only if

¶ y- z ¶≥ 2a

The statement that a finite or infinite number of spheres Sa (y) of fixed radius a can be packed in S means that each sphere Sa (y) is contained in S and that no two such spheres overlap.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 4 , Issue 1 , December 1958 , pp. 22 - 25
Copyright
Copyright © Glasgow Mathematical Journal Trust 1958

References

1.Rankin, R. A., On sums of powers of linear forms I, Ann. of Math., 50 (1949), 691–698.CrossRefGoogle Scholar
2.Rankin, R. A., On sums of powers of linear forms II, Ann. of Math., 50 (1949), 699–704.CrossRefGoogle Scholar
3.Rankin, R. A., On packings of spheres in Hilbert space, Proc. Glasgow Math. Assoc., 2 (1955), 145–146.CrossRefGoogle Scholar