No CrossRef data available.
Article contents
Pairs of quadratic forms modulo one
Published online by Cambridge University Press: 18 May 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let s be a natural number, s ≥ 2. We seek a positive number λ(s) with the following property:
Let ε > 0. Let Q1(x1, …, xs), Q2(x1, …, xs) be real quadratic forms, then for N > C1(s, ε) we have
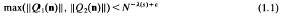
for some integers n1, …, ns,
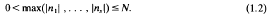
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1993
References
REFERENCES
2.Baker, R. C. and Harman, G., Small fractional parts of quadratic and additive forms, Math. Proc. Camb. Phil Soc. 90 (1981), 5–12.CrossRefGoogle Scholar
3.Baker, R. C. and Harman, G., Small fractional parts of quadratic forms, Proc. Edinburgh Math. Soc., 25 (1982), 269–277.Google Scholar
4.Baker, R. C. and Schäffer, S.. Pairs of additive quadratic forms modulo one. Submitted to Acta Arith.Google Scholar
6.Danicic, I., The distribution (mod 1) of pairs of quadratic forms with integer variables, J. London Math. Soc. 42 (1967), 618–623.CrossRefGoogle Scholar
7.Davenport, H., Indefinite quadratic forms in many variables, Mathematika 3 (1956), 81–101.Google Scholar
8.Davenport, H., Indefinite quadratic forms in many variables II, Proc. London Math. Soc. (3), 8 (1958), 109–126.Google Scholar
9.Heath-Brown, D. R.. Small solutions of quadratic congruences, II. Mathematika, to appear.Google Scholar
10.Schinzel, A., Schlickewei, H. P. and Schmidt, W. M., Small solutions of quadratic congruences and small fractional parts of quadratic forms, Acta Arith. 37 (1980), 241–248.Google Scholar
11.Schmidt, W. M., Small fractional parts of polynomials, Regional Conference Series No. 32, American Math. Soc, Providence 1977.Google Scholar

