Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T07:01:27.825Z Has data issue: false hasContentIssue false
  • English
  • Français

PBW THEOREMS AND FROBENIUS STRUCTURES FOR QUANTUM MATRICES

Published online by Cambridge University Press:  01 September 2007

FABIO GAVARINI
FABIO GAVARINI*
Affiliation:
Università di Roma “Tor Vergata” – Dipartimento di Matematica Via della Ricerca Scientifica 1, I-00133 Roma – ITALY e-mail: gavarini@mat.uniromal
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

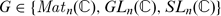Let , let 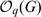be the quantum function algebra – over 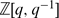– associated to G, and let 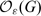be the specialisation of the latter at a root of unity ϵ, whose order ℓ is odd. There is a quantum Frobenius morphism that embeds 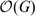the function algebra of G, in 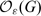as a central Hopf subalgebra, so that 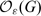is a module over 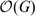. When 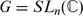, it is known by [3], [4] that (the complexification of) such a module is free, with rank ℓdim(G). In this note we prove a PBW-like theorem for 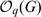, and we show that – when G is Matn or GLn – it yields explicit bases of 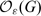over 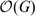. As a direct application, we prove that 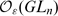and 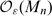are free Frobenius extensions over 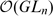and 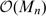, thus extending some results of [5].

Keywords

Primary 20G42Secondary 81R50
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 49 , Issue 3 , September 2007 , pp. 479 - 488
Copyright
Copyright © Glasgow Mathematical Journal Trust 2007

References

REFERENCES

1.Andersen, H. H., Kexin, W. and Polo, P., Representations of quantum algebras, Invent. Math. 104 (1991), 1–59.CrossRefGoogle Scholar
2.Bergman, G. M., The diamond lemma for ring theory, Adv. Math. 29 (1978), 178–218.CrossRefGoogle Scholar
3.Brown, K. A. and Gordon, I., The ramifications of the centres: quantised function algebras at roots of unity, Proc. London Math. Soc. (3) 84 (2002), 147–178.CrossRefGoogle Scholar
4.Brown, K. A., Gordon, I. and Stafford, J. T., is a free module over preprint http://arxiv.org/abs/math.QA/0007179 (2000), 3 pages.Google Scholar
5.Brown, K. A., Gordon, I. and Stroppel, C., Cherednik, Hecke and quantum algebras as free modules and Calabi-Yau extensions preprint http://arxiv.org/abs/math.RT/0607170 (2006), 31 pages.Google Scholar
6.Chari, V. and Pressley, A., A guide to quantum groups (Cambridge University Press 1994).Google Scholar
7.De Concini, C. and Lyubashenko, V., Quantum function algebra at roots of 1, Adv. Math. 108 (1994), 205–262.CrossRefGoogle Scholar
8.Dabrowski, L., Reina, C. and Zampa, A., A(SLq(2)) at roots of unity is a free module over A(SL(2)) Lett. Math. Phys. 52 (2000), 339–342.CrossRefGoogle Scholar
9.Gavarini, F., Quantum function algebras as quantum enveloping algebras, Comm. Algebra 26 (1998), 1795–1818.CrossRefGoogle Scholar
10.Koelink, H. T., On *-representations of the Hopf *-algebra associated with the quantum group U q(n), Compositio Math. 77 (1992), 199–231.Google Scholar
11.Levasseur, T. and Stafford, J. T., The quantum coordinate ring of the special linear group, J. Pure Appl. Algebra 86 (1993), 181–186.CrossRefGoogle Scholar
12.Parshall, B. and Wang, J., Quantum linear groups, Mem. Amer. Math. Soc. 89 (1991), no. 439.Google Scholar