Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T06:42:37.087Z Has data issue: false hasContentIssue false
  • English
  • Français

PERTURBATION OF BANACH SPACE OPERATORS WITH A COMPLEMENTED RANGE

Part of: General theory of linear operators

Published online by Cambridge University Press:  21 March 2017

B. P. DUGGAL  and
C. S. KUBRUSLY
B. P. DUGGAL
Affiliation:
8 Redwood Grove, Northfield Avenue, Ealing, London W5 4SZ, United Kingdom e-mail: bpduggal@yahoo.co.uk
C. S. KUBRUSLY
Affiliation:
Catholic University of Rio de Janeiro, 22453-900, Rio de Janeiro, RJ, Brazil E-mail: carlos@ele.puc-rio.br
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 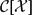${\mathcal C}[{\mathcal X}]$ be any class of operators on a Banach space 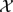${\mathcal X}$, and let 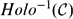${Holo}^{-1}({\mathcal C})$ denote the class of operators A for which there exists a holomorphic function f on a neighbourhood 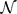${\mathcal N}$ of the spectrum σ(A) of A such that f is non-constant on connected components of 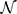${\mathcal N}$ and f(A) lies in 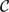${\mathcal C}$. Let 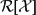${{\mathcal R}[{\mathcal X}]}$ denote the class of Riesz operators in 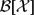${{\mathcal B}[{\mathcal X}]}$. This paper considers perturbation of operators 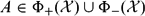$A\in\Phi_{+}({\mathcal X})\Cup\Phi_{-}({\mathcal X})$ (the class of all upper or lower [semi] Fredholm operators) by commuting operators in 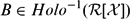$B\in{Holo}^{-1}({\mathcal R}[{\mathcal X}])$. We prove (amongst other results) that if πB(B) = ∏mi = 1(B − μi) is Riesz, then there exist decompositions 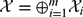${\mathcal X}=\oplus_{i=1}^m{{\mathcal X}_i}$ and 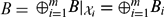$B=\oplus_{i=1}^m{B|_{{\mathcal X}_i}}=\oplus_{i=1}^m{B_i}$ such that: (i) If λ ≠ 0, then 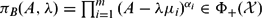$\pi_B(A,\lambda)=\prod_{i=1}^m{(A-\lambda\mu_i)^{\alpha_i}} \in\Phi_{+}({\mathcal X})$ (resp., 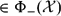$\in\Phi_{-}({\mathcal X})$) if and only if 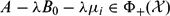$A-\lambda B_0-\lambda\mu_i\in\Phi_{+}({\mathcal X})$ (resp., 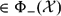$\in\Phi_{-}({\mathcal X})$), and (ii) (case λ = 0) 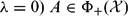$A\in\Phi_{+}({\mathcal X})$ (resp., 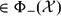$\in\Phi_{-}({\mathcal X})$) if and only if 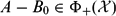$A-B_0\in\Phi_{+}({\mathcal X})$ (resp., 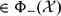$\in\Phi_{-}({\mathcal X})$), where B0 = ⊕mi = 1(Bi − μi); (iii) if 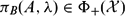$\pi_B(A,\lambda)\in\Phi_{+}({\mathcal X})$ (resp., 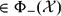$\in\Phi_{-}({\mathcal X})$) for some λ ≠ 0, then 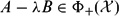$A-\lambda B\in\Phi_{+}({\mathcal X})$ (resp., 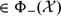$\in\Phi_{-}({\mathcal X})$).

MSC classification

Primary: 47A53: (Semi-) Fredholm operators; index theories
Secondary: 47A10: Spectrum, resolvent
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 59 , Issue 3 , September 2017 , pp. 659 - 671
Copyright
Copyright © Glasgow Mathematical Journal Trust 2017 

References

REFERENCES

1. Aiena, P., Fredholm and Local Spectral Theory, with Applications to Multipliers (Kluwer-Springer, New York, 2004).Google Scholar
2. Aiena, P. and Müller, V., The localized single-valued extension property and Riesz operators, Proc. Amer. Math. Soc. 143 (2015), 2051–2055.Google Scholar
3. Albrecht, E. and Mehta, R. D., Some remarks on local spectral theory, J. Operator Theory. 12 (1984), 285–317.Google Scholar
4. Buoni, J. J., Harte, R. E. and Wickstead, A. W., Upper and lower Fredholm spectra, Proc. Amer. Math. Soc. 66 (1977), 309–314.Google Scholar
5. Campbell, S. L. and Faulkner, G. D., Operators on Banach spaces with complemented ranges, Acta Math. Acad. Sci. Hungar. 35 (1980), 123–128.Google Scholar
6. Djordjević, D. S., Duggal, B. P. and Živković-Zlatanović, S. Č., Perturbations, quasinilpotent equivalence and communicating operators, Math. Proc. Royal Irish Acad. 115 A (2015), 1–14.Google Scholar
7. Djordjević, D. S. and Rakočević, V., Lectures on Generalized Inverse, Faculty of Science and Mathematics (University of Niš, Niš, 2008).Google Scholar
8. Gilfeather, F., The structure and asymptotic behaviour of polynomially compact operators, Proc. Amer. Math. Soc. 25 (1970), 127–134.Google Scholar
9. Harte, R. E., Invertibility and Singularity, Vol 109 (Marcel Dekker, New York, 1988).Google Scholar
10. Holub, J. R., On perturbation of operators with complemented range, Acta Math. Hung. 44 (1984), 269–273.CrossRefGoogle Scholar
11. Jeribi, A. and Moalla, N., Fredholm operators and Riesz theory for polynomially compact operators, Acta Applicandae Math. 90 (2006), 227–247.CrossRefGoogle Scholar
12. Kubrusly, C. S. and Duggal, B. P., Upper-lower and left-right semi-Fredholmness, Bull. Belg. Math. Soc. Simon Stevin, 23 (2016), 217–233.Google Scholar
13. Latrach, K., Martin Padi, J. and Taoudi, M. A., A characterization of polynomially Riesz strongly continuous semigroups, Comment. Math. Carolina 47 (2006), 275–289.Google Scholar
14. Laursen, K. B. and Neumann, M. N., Introduction to Local Spectral Theory (Clarendon Press, Oxford, 2000).Google Scholar
15. Müller, V., Spectral Theory of Linear Operators – and Spectral Systems in Banach Algebras, 2nd edn. (Birkhäuser, Basel, 2007).Google Scholar
16. Živkovic-Zlatanović, S. Č., Djordjević, D. S., Harte, R. E. and Duggal, B. P., On polynomially Riesz operators, Filomat 28:1 (2014), 197–205.Google Scholar