Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T06:44:26.337Z Has data issue: false hasContentIssue false
  • English
  • Français

PERTURBATIONS FROM INDEFINITE SYMMETRIC ELLIPTIC BOUNDARY VALUE PROBLEMS

Part of: Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  08 February 2017

LIANG ZHANG  and
XIANHUA TANG
LIANG ZHANG
Affiliation:
School of Mathematical Sciences, University of Jinan, Jinan, Shandong 250022, P.R. China e-mail: mathspaper2012@126.com
XIANHUA TANG
Affiliation:
School of Mathematics and Statistics, Central South University, Changsha, Hunan 410083, P.R. China
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we study the multiplicity of solutions for the following problem: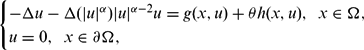

$$\begin{equation*} \begin{cases} -\Delta u-\Delta(|u|^{\alpha})|u|^{\alpha-2}u=g(x,u)+\theta h(x,u), \ \ x\in \Omega,\\ u=0, \ \ x\in \partial\Omega, \end{cases} \end{equation*}$$
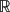where α ≥ 2, Ω is a smooth bounded domain in ${\mathbb{R}}$N, θ is a parameter and g, h ∈ C($\bar{\Omega}$ × 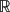${\mathbb{R}}$). Under the assumptions that g(x, u) is odd and locally superlinear at infinity in u, we prove that for any j ∈ 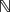$\mathbb{N}$ there exists ϵj > 0 such that if |θ| ≤ ϵj, the above problem possesses at least j distinct solutions. Our results generalize some known results in the literature and are new even in the symmetric situation.

MSC classification

Primary: 35B20: Perturbations
Secondary: 35J20: Variational methods for second-order elliptic equations 35J62: Quasilinear elliptic equations
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 59 , Issue 3 , September 2017 , pp. 635 - 648
Copyright
Copyright © Glasgow Mathematical Journal Trust 2017 

References

REFERENCES

1. Adachi, S. and Watanabe, T., Uniqueness of the ground state solutions of quasilinear Schrödinger equations, Nonlinear Anal. 75 (2012), 819–833.Google Scholar
2. Bahri, A. and Berestycki, H., A perturbation method in critical point theory and applications, Trans. Amer. Math. Soc. 267 (1981), 1–32.Google Scholar
3. Bahri, A. and Lions, P. L., Morse-index of some min-max critical points. I. Application to multiplicity results, Comm. Pure Appl. Math. 41 (1988), 1027–1037.Google Scholar
4. Clapp, M., Ding, Y. H. and Hernández-Linares, S., Strongly indefinite functionals with perturbed symmetries and multiple solutions of nonsymmetric elliptic systems, Electron. J. Differ. Equ. 100 (2004), 1–14.Google Scholar
5. Colin, M. and Jeanjean, L., Solutions for a quasilinear schrödinger equation: A dual approach, Nonlinear Anal. 56 (2004), 213–226.Google Scholar
6. Degiovanni, M. and Lancelotti, S., Perturbations of even nonsmooth functionals, Differ. Integral Equ., 8 (1995), 981–992.Google Scholar
7. Kurihara, S., Large-amplitude quasi-solitons in superfluid films, J. Phys. Soc. Japan 50 (1981), 3262–3267.Google Scholar
8. Kajikiya, R., Multiple solutions of sublinear Lane-Emden elliptic equations, Calc. Var. Partial Differ. Equ. 26 (2006), 29–48.Google Scholar
9. Laedke, E. W., Spatschek, K. H. and Stenflo, L., Evolution theorem for a class of perturbed envelope soliton solutions, J. Math. Phys. 24 (1983), 2764–2769.CrossRefGoogle Scholar
10. Li, S. J. and Liu, Z. L., Perturbations from elliptic boundary problems, J. Differ. Equ. 185 (2002), 271–280.CrossRefGoogle Scholar
11. Liu, J. Q., Wang, Y. Q. and Wang, Z. Q., Soliton solutions for quasilinear Schrödinger equations II, J. Differ. Equ. 187 (2003), 473–493.Google Scholar
12. Liu, J. Q. and Wang, Z. Q., Soliton solutions for quasilinear Schrödinger equations I, Proc. Amer. Math. Soc. 131 (2003), 441–448.Google Scholar
13. Liu, J. Q., Wang, Y. and Wang, Z. Q., Solutions for quasilinear Schrödinger equations via the Nehari method, Comm. Partial Differ. Equ. 29 (2004), 879–892.Google Scholar
14. Liu, X. Q., Liu, J. Q. and Wang, Z. Q., Quasilinear elliptic equations with critical growth via perturbation method, J. Differ. Equ. 254 (2013), 102–124.Google Scholar
15. Liu, X. Q., Liu, J. Q. and Wang, Z. Q., Quasilinear elliptic equations via perturbation method, Proc. Amer. Math. Soc. 141 (2013), 253–263.Google Scholar
16. Liu, X. Q. and Zhao, F. K., Existence of infinitely many solutions for quasilinear elliptic equations perturbed from symmetry, Adv. Nonlinear Stud. 13 (2013), 965–978.Google Scholar
17. Nakamura, A., Damping and modification of exciton solitary waves, J. Phys. Soc. Japan 42 (1977), 1824–1835.Google Scholar
18. Rabinowitz, P., Multiple critical points of perturbed symmetric functionals, Trans. Amer. Math. Soc. 272 (1982), 753–769.Google Scholar
19. Rabinowitz, P. H., Minimax methods in critical point theory with applications to differential equations, in CBMS regional conference series in mathematics, vol. 65 (American Mathematical Society, Providence, RI, 1986).Google Scholar
20. Ruiz, D. and Siciliano, G., Existence of ground states for a modified nonlinear Schrödinger equation, Nonliearity 23 (2010), 1221–1233.Google Scholar
21. Salvatore, A., Multiple solutions for perturbed elliptic equations in unbounded domains, Adv. Nonlinear Stud. 3 (2003), 1–23.CrossRefGoogle Scholar
22. Schechter, M. and Zou, W., Infinitely many solutions to perturbed elliptic equations, J. Funct. Anal. 228 (2005), 1–38.Google Scholar
23. Tarsi, C., Perturbation from symmetry and multiplicity of solutions for strongly indefinite elliptic systems, Adv. Nonlinear Stud. 7 (2007), 1–30.Google Scholar
24. Willem, M., Minimax theorems (Birkhäuser, Berlin, 1996).Google Scholar
25. Wu, X., Multiple solutions for quasilinear Schrödinger equations with a parameter, J. Differ. Equ. 256 (2014), 2619–2632.Google Scholar
26. Wu, X. and Wu, K., Existence of positive solutions, negative solutions and high energy solutions for quasilinear elliptic equations on ${\mathbb{R}}$ N , Nonlinear Anal. RWA 16 (2014), 48–64.Google Scholar
27. Zhang, J., Tang, X. H. and Zhang, W., Infinitely many solutions of quasilinear Schrödinger equation with sign-changing potential, J. Math. Anal. Appl. 420 (2014), 1762–1775.Google Scholar
28. Zhang, L., Tang, X. H. and Chen, Y., Infinitely many solutions for quasilinear Schrödinger equations under broken symmetry situations, Topol. Methods Nonlinear Anal. doi: 10.12775/TMNA.2016.057.Google Scholar
29. Zhang, L., Tang, X. H. and Chen, Y., Infinitely many solutions for indefinite quasilinear Schrödinger equations under broken symmetry situations, Math. Methods Appl. Sci. doi: 10.1002/mma.4030.Google Scholar