Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-15T15:21:38.815Z Has data issue: false hasContentIssue false
  • English
  • Français

Positive matrices and eigenvectors†

Published online by Cambridge University Press:  18 May 2009

C. R. Putnam
C. R. Putnam
Affiliation:
Purdue University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For i, j = 1, 2, …, let aij be real. A matrix A = (aij) will be called positive (A>0) or non-negative (A≧0) according as, for all i and j, aij>0 or aij≧0 respectively. Correspondingly, a real vector x = (x1, x2, …) will be called positive (x>0) or non-negative (x≧0) according as, for all i, xi>0 or x≧0. A matrix A is said to be bounded if ∥ Ax ∥ ≦M ∥ x ∥ holds for some constant M, 0 ≦ M < ∞, and all x in the Hilbert space H of real vectors x = (x1, x2, …) satisfying 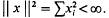. The least such constant M is denoted by ∥ A ∥. If x and y belong to H, then (x, y) will denote as usual the scalar product Σxiyi. Whether or not x is in H, or A is bounded, y = Ax will be considered as defined by

whenever each of the series of (1) is convergent.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 6 , Issue 1 , January 1963 , pp. 27 - 30
Copyright
Copyright © Glasgow Mathematical Journal Trust 1963

References

REFERENCES

1.Bonsall, F. F., Endomorphisms of partially ordered vector spaces, J. London Math. Soc. 30 (1955), 133–144.CrossRefGoogle Scholar
2.Bonsall, F. F., Endomorphisms of a partially ordered vector space without order unit, F. F. Bonsall 30 (1955), 144–153.Google Scholar
3.Bonsall, F. F., Linear operators in complete positive cones, Proc. London Math. Soc., Ser. 3, 8 (1958), 53–75.CrossRefGoogle Scholar
4.Frobenius, G., Ueber Matrizen aus positiven Elementen, Sitzungsberichte Preuss. Akad. Wiss. (Berlin, 1908), 471–476; (1909), 514–518.Google Scholar
5.Frobenius, G., Ueber Matrizen aus nicht negativen Elementen, G. Frobenius. (1912), 456–477.Google Scholar
6.Hardy, G. H., Littlewood, J. E. and Polya, G., Inequalities (Cambridge, 1952).Google Scholar
7.Hartman, P. and Wintner, A., The spectra of Toeplitz matrices, Amer.J. Math. 76 (1954), 867–882.CrossRefGoogle Scholar
8.Karlin, S., Positive operators, J. Math, and Mech. 8 (1959), 907–937.Google Scholar
9.Kato, T., On the Hilbert matrix, Proc. Amer. Math. Soc. 8 (1957), 73–81.CrossRefGoogle Scholar
10.Kato, T., On positive eigenvectors of positive infinite matrices, Comm. Pure and Applied Math. 11 (1958), 573–586.CrossRefGoogle Scholar
11.Krein, M. G. and Rutman, M. A., Linear operators leaving invariant a cone in a Banach space Uspehi Mat. Nauk (N. S.) 3, No. 1 (23) (1948), 3–95, Amer. Math. Soc. Trans. No. 26.Google Scholar
12.Magnus, W., On the spectrum of Hilbert's matrix, Amer. J. Math. 72 (1950), 699–704.CrossRefGoogle Scholar
13.Perron, O., Zur Theories der Matrices, Math. Annalen 64 (1907), 248–263.CrossRefGoogle Scholar
14.Putnam, C. R., On bounded matrices with non-negative elements, Canadian J. Math. 10 (1958), 587–591.CrossRefGoogle Scholar
15.Putnam, C. R., A note on non-negative matrices, C. R. Putham. 13 (1961), 59–62.Google Scholar
16.Rutman, M. A., Sur les opérateurs totalement continus linéaires laissant invariant un certain cone, Mat. Sbornik (N. S.) 8, no. 1 (50) (1940), 77–96.Google Scholar
17.Rosenblum, M., On the Hilbert matrix, I, Proc. Amer. Math. Soc. 9 (1958), 137–140.Google Scholar
18.Taussky, O., A remark concerning the characteristic roots of the finite segments of the Hilbert matrix, Quart. J. Math., Oxford Ser., vol. 20 (1949), 80–83.CrossRefGoogle Scholar
19.Taussky, O., Research Problem 60–3–12, Bull. Amer. Math. Soc.Google Scholar