Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Taghavi, Ali
Afrouzi, Ghasem
and
Ghorbani, Horieh
2014.
Existence of nontrivial solution for elliptic systems involving the p(x)-Laplacian.
Studia Scientiarum Mathematicarum Hungarica,
Vol. 51,
Issue. 2,
p.
213.
Afrouzi, G. A.
Shakeri, S.
and
Chung, N. T.
2015.
Existence of positive solutions for variable exponent elliptic systems with multiple parameters.
Afrika Matematika,
Vol. 26,
Issue. 1-2,
p.
159.
Guefaifia, Rafik
and
Boulaaras, Salah
2018.
Existence of positive solutions for a class of $$\left( p\left( x\right) , q\left( x\right) \right) $$-Laplacian systems.
Rendiconti del Circolo Matematico di Palermo Series 2,
Vol. 67,
Issue. 1,
p.
93.
Boulaaras, Salah
Guefaifia, Rafik
and
Kabli, Sarah
2019.
An asymptotic behavior of positive solutions for a new class of elliptic systems involving of $$\left( p\left( x\right) ,q\left( x\right) \right) $$ p x , q x -Laplacian systems.
Boletín de la Sociedad Matemática Mexicana,
Vol. 25,
Issue. 1,
p.
145.
Sousa, J. Vanterler da C.
Bouali, Tahar
and
Guefaifia, Rafik
2024.
Fractional Laplacian Elliptic Systems with Multiple Parameters.
Complex Analysis and Operator Theory,
Vol. 18,
Issue. 7,
Zhang, Zhenfeng
Vetro, Calogero
An, Tianqing
and
Chen, Wei
2025.
Existence Results for Neumann Problem with Critical Sobolev–Hardy Exponent and Choquard-Type Nonlinearity.
Fractal and Fractional,
Vol. 9,
Issue. 9,
p.
574.
Vanterler da Costa Sousa, José
Tavares, Leandro S.
and
Chung, Nguyen Thanh
2025.
Existence of positive weak solutions for fractional Laplacian elliptic systems.
Georgian Mathematical Journal,

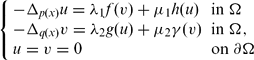
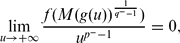
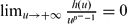 and
and 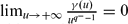 . In particular, we do not assume any sign conditions on
. In particular, we do not assume any sign conditions on 