Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Peng, Chaoquan
and
Yang, Jianfu
2010.
Positive solution for asymptotically linear elliptic systems.
Mathematical Methods in the Applied Sciences,
Vol. 33,
Issue. 6,
p.
758.
PENG, CHAOQUAN
2010.
ASYMPTOTICALLY LINEAR ELLIPTIC SYSTEMS WITH PARAMETERS.
Glasgow Mathematical Journal,
Vol. 52,
Issue. 2,
p.
383.
Chhetri, Maya
and
Girg, Petr
2014.
Asymptotically linear systems near and at resonance.
Boundary Value Problems,
Vol. 2014,
Issue. 1,
Hai, D. D.
and
Williams, J. L.
2015.
Positive Radial Solutions for a Class of Singular p-Laplacian Systems in a Ball.
Mediterranean Journal of Mathematics,
Vol. 12,
Issue. 3,
p.
791.
Chhetri, Maya
and
Girg, Petr
2016.
Asymptotically linear system of three equations near resonance.
Journal of Differential Equations,
Vol. 261,
Issue. 10,
p.
5900.
Chhetri, M.
and
Girg, P.
2017.
A global bifurcation result for a class of semipositone elliptic systems.
Journal of Mathematical Analysis and Applications,
Vol. 453,
Issue. 1,
p.
255.


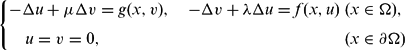
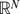 ,
, 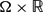 and asymptotically linear at infinity.
and asymptotically linear at infinity.