Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-15T19:21:41.477Z Has data issue: false hasContentIssue false
  • English
  • Français

Positive solutions of integrodifferential and difference equations with unbounded delay

Published online by Cambridge University Press:  18 May 2009

Thomas Kiventidis
Thomas Kiventidis
Affiliation:
Department of MathematicsUniversity of ThessalonikiThessaloniki54006 Greece
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We establish a necessary and sufficient condition for the existence of a positive solution of the integrodifferential equation

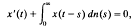
where nis an increasing real-valued function on the interval [0, α); that is, if and only if the characteristic equation

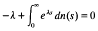
admits a positive root.

Consider the difference equation 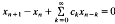, where 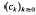is a sequence of non-negative numbers. We prove this has positive solution if and only if the characteristic equation 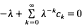admits a root in (0, 1). For general results on integrodifferential equations we refer to the book by Burton [1] and the survey article by Corduneanu and Lakshmikantham [2]. Existence of a positive solution and oscillations in integrodifferential equations or in systems of integrodifferential equations recently have been investigated by Ladas, Philos and Sficas [5], Györi and Ladas [4], Philos and Sficas [12], Philos [9], [10], [11].

Recently, there has been some interest in the existence or the non-existence of positive solutions or the oscillation behavior of some difference equations. See Ladas, Philos and Sficas [6], [7].

The purpose of this paper is to investigate the positive solutions of integrodifferential equations (Section 1) and difference equations (Section 2) with unbounded delay. We obtain also some results for integrodifferential and difference inequalities.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 35 , Issue 1 , January 1993 , pp. 105 - 113
Copyright
Copyright © Glasgow Mathematical Journal Trust 1993

References

REFERENCES

1.Burton, T. A., Voltera integral and differential equations (Academic Press, 1983).Google Scholar
2.Corduneanu, C. and Lakshmikantham, V., Equations with unbounded delay: A survey, Nonlinear Analysis TMA 4 (1980), 831–877.CrossRefGoogle Scholar
3.Cushing, J. M., Integrodifferential equations and delay models in population dynamics, Lecture Notes in Biomathematics, Vol. 20 (Springer-Verlag, 1977).CrossRefGoogle Scholar
4.Györi, I. and Ladas, G., Positive solutions of integrodifferential equations with unbounded delay, to appear.Google Scholar
5.Ladas, G., Philos, Ch. G. and Sficas, Y. G., Oscillations of integrodifferential equations, Differential and Integral Equations, to appear.Google Scholar
6.Ladas, G., Philos, Ch. G. and Sficas, Y. G., Necessary and sufficient condition for the oscillation of difference equations, Libertas Math. 9 (1989), 121–125.Google Scholar
7.Ladas, G., Philos, Ch. G. and Sficas, Y. G., Existence of positive solutions for certain difference equations, Utilitas Math., to appear.Google Scholar
8.Ladas, G., Sficas, Y. G. and Stavroulakis, I. P.Necessary and sufficient conditions for oscillations, Amer. Math. Monthly 90 (1983) 637–640.CrossRefGoogle Scholar
9.Philos, Ch. G., Oscillatory behavior of systems of integrodifferential equations Bull. Soc. Math. Grèce (N.S) 29 (1988), 131–141.Google Scholar
10.Philos, Ch. G., Oscillation and nonoscillation in integrodifferential equations, to appear.Google Scholar
11.Philos, Ch. G., Positive solution of integrodifferential equations, to appear.Google Scholar
12.Philos, Ch. G. and Sficas, Y. G., On the existence of positive solutions of integrodifferential equations, Applicable Anal. 36 (1990), 189–210.CrossRefGoogle Scholar