Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T06:06:26.874Z Has data issue: false hasContentIssue false
  • English
  • Franรงais

THE PRIME IDEALS AND SIMPLE MODULES OF THE UNIVERSAL ENVELOPING ALGEBRA U(๐”Ÿโ‹‰V2)

Part of: Modules, bimodules and ideals Lie algebras and Lie superalgebras Chain conditions, growth conditions, and other forms of finiteness

Published online by Cambridge University Press:ย  29 July 2019

VOLODYMYR V. BAVULA  and
TAO LU
VOLODYMYR V. BAVULA
Affiliation:
Department of Pure Mathematics, University of Sheffield, Sheffield, S3 7RH, UK e-mail: v.bavula@sheffield.ac.uk
TAO LU
Affiliation:
School of Mathematical Sciences, Huaqiao University, Quanzhou, Fujian, 362021, China e-mail: lutao.sdu@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let ๐”Ÿ be the Borel subalgebra of the Lie algebra ๐”ฐ๐”ฉ2 and V2 be the simple two-dimensional ๐”ฐ๐”ฉ2-module. For the universal enveloping algebra 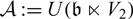$\[{\cal A}: = U(\gb \ltimes {V_2})\]$ of the semi-direct product ๐”Ÿโ‹‰V2 of Lie algebras, the prime, primitive and maximal spectra are classified. Please approve edit to the sentence โ€œThe sets of completely primeโ€ฆโ€.The sets of completely prime ideals of 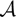$\[{\cal A}\]$ are described. The simple unfaithful 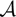$\[{\cal A}\]$-modules are classified and an explicit description of all prime factor algebras of 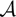$\[{\cal A}\]$ is given. The following classes of simple U(๐”Ÿโ‹‰V2)-modules are classified: the Whittaker modules, the ๐•‚[X]-torsion modules and the ๐•‚[E]-torsion modules.

MSC classification

Primary: 17B10: Representations, algebraic theory (weights)
Secondary: 16D25: Ideals 16D60: Simple and semisimple modules, primitive rings and ideals 16D70: Structure and classification (except as in ), direct sum decomposition, cancellation 16P50: Localization and Noetherian rings
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 62 , Special Issue S1: Workshop on Nonassociative algebras and their applications , December 2020 , pp. S77 - S98
Copyright
Copyright ยฉ Glasgow Mathematical Journal Trust 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bavula, V. V., The simple D[X, Y; ฯƒ, a]-modules, Ukrainian Math. J. 44 (1992), 1628โ€“1644.CrossRefGoogle Scholar
Bavula, V. V., Generalized Weyl algebras and their representations, St. Petersburg Math. J. 4(1) (1993), 71โ€“92.Google Scholar
Bavula, V. V., Tensor homological minimal algebras, global dimension of the tensor product of algebras and of generalized Weyl algebras, Bull. Sci. Math. 120(3) (1996), 293โ€“335.Google Scholar
Bavula, V. V., Global dimension of generalized Weyl algebras, in Representation theory of algebras (Cocoyoc, 1994), CMS Conf. Proc., 18, American Mathematics Society, Providence, RI (1996) 81โ€“107.Google Scholar
Bavula, V. V., Classification of the simple modules of the quantum Weyl algebra and the quantum plane, in Quantum groups and quantum spaces (Warsan, 1995), vol. 40 (Banach Center Publ., Polish Acad. Sci., Warsaw, 1997), 193โ€“201.Google Scholar
Bavula, V. V. and van Oystaeyen, F., The simple modules of certain generalized crossed products, J. Algebra 194 (1997), 521โ€“566.CrossRefGoogle Scholar
Bavula, V. V., The simple modules of Ore extensions with coefficients from a Dedekind ring, Comm. Algebra 27(6) (1999), 2665โ€“2699.CrossRefGoogle Scholar
Bavula, V. and van Oystaeyen, F., Simple modules of the Wittenโ€“Woronowicz algebra, J. Algebra 271 (2004), 827โ€“845.CrossRefGoogle Scholar
Bavula, V. V. and Lu, T., The prime spectrum and simple modules over the quantum spatial ageing algebra, Algebr. Represent. Theory 19 (2016), 1109โ€“1133.CrossRefGoogle Scholar
Benkart, G., Lopes, S. A. and Ondrus, M., A parametric family of subalgebras of the Weyl algebra II. Irreducible modules, in Algebraic and combinatorial approaches to representation theory (Chari, V., Greenstein, J., Misra, K. C., Raghavan, K. N. and Viswanath, S., Editors), Contemp. Math., vol. 602 (American Mathematics Society, Providence, RI, 2013), 73โ€“98.Google Scholar
Block, R. E., The irreducible representations of the Lie algebra (2) and of the Weyl algebra, Adv. Math. 39 (1981), 69โ€“110.CrossRefGoogle Scholar
Henkel, M. and Stoimenov, S., On non-local representations of the ageing algebra, Nuclear Phys. B 847(3) (2011), 612โ€“627.Google Scholar
Lรผ, R., Mazorchuk, V. and Zhao, K., Classification of simple weight modules over the 1-spatial ageing algebra, Algebr. Represent. Theory 18(2) (2015), 381โ€“395.CrossRefGoogle Scholar
McConnell, J. C. and Robson, J. C., Noncommutative noetherian rings, Graduate Studies in Mathematics, vol. 30 (American Mathematical Society, Providence, RI, 2001).Google Scholar
Sigurdsson, G., Differential operator rings whose prime factors have bounded Goldie dimension, Arch. Math. (Basel) 42(4) (1984), 348โ€“353.Google Scholar
Stoimenov, S. and Henkel, M., Non-local space-time transformations generated from the ageing algebra, in Lie theory and its applications in physics (Dobrev, V., Editor) Springer Proceedings in Mathematics & Statistics, vol. 36 (Springer, Tokyo, 2013), 369โ€“379.CrossRefGoogle Scholar
Stoimenov, S. and Henkel, M., Non-local representations of the ageing algebra in higher dimensions, J. Phys. A 46(24) (2013), 245004, 18pp.CrossRefGoogle Scholar