Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-16T16:41:32.389Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasidistinguished countable enlargements of normed spaces

Published online by Cambridge University Press:  18 May 2009

S. A. Saxon  and
L. M. Sànchez Ruiz
S. A. Saxon
Affiliation:
Department of Mathematics, University of Florida, PO Box 118000, Gainesville, FL 32611-8000, U.S.A.
L. M. Sànchez Ruiz
Affiliation:
EUITI, Departamento de Matemática Aplicada, Universidad Polytécnica de Valencia, 46071 Valencia, Spain
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If E is a Hausdorff locally convex space and M is an 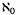-dimensional subspace of the algebraic dual E* that is transverse to the continuous dual E′, then, according to [7], the Mackey topology τ(E, E′ + M) is a countable enlargement (CE) of τ(E, E′) [or of E]. Much is still unknown as to when CEs preserve barrelledness (cf. [14]). E is quasidistinguished (QD) if each bounded subset of the completion Ê is contained in the completion of a bounded subset of E [12]. Clearly, each normed space is QD, and Tsirulnikov [12] asked if each CE of a normed space must be a QDCE, i.e., must preserve the QD property. Since CEs preserve metrizability (but not normability), her question was whether metrizable spaces so obtained must be QD, and was moderated by Amemiya's negative answer (cf. [5, p. 404]) to Grothendieck's query, who had asked if all metrizable spaces are QD, having proved the separable ones are [4].

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 38 , Issue 1 , January 1996 , pp. 65 - 68
Copyright
Copyright © Glasgow Mathematical Journal Trust 1996

References

REFERENCES

1.Catálan, F. X. and Tweddle, I., Countable enlargements of norm topologies and the quasidistinguished property. Glasgow Math. J. 35 (1993), 235–238.CrossRefGoogle Scholar
2.van Douwen, E. K., The integers and topology, pp. 111–168 in Handbook of set-theoretic topology, (eds.: Kunen, K. and Vaughan, J. E.). (North Holland 1984).CrossRefGoogle Scholar
3.Engelking, R., General Topology. PWN 1977.Google Scholar
4.Grothendieck, A., Sur les espaces (F) et (DF). Summa Brasil. Math. 3 (1954) 57–123.Google Scholar
5.Köthe, G., Topological Vector Spaces (Springer Verlag, 1969).Google Scholar
6.Robertson, A. P. and Robertson, W. J., Topological Vector Spaces (Cambridge 1973).Google Scholar
7.Robertson, W. J, Tweddle, I. and Yeomans, F. E., On the stability of barrelled topologies III. Bull. Austr. Math. Soc. 22 (1980), 99–112.CrossRefGoogle Scholar
8.Saxon, S. A., The codensity character of topological vector spaces, in Topological Vector Spaces, Algebras & Related Areas (eds. Lau, A. and Tweddle, I.), (Longman, 1994), 24–36.Google Scholar
9.Saxon, S. A. and Ruiz, L. M. Sánchez, Optimal cardinals for metrizable barrelled spaces. J. London Math. Soc. (2) 51 (1995), 137–147.CrossRefGoogle Scholar
10.Saxon, S. A. and Ruiz, L. M Sánchez, Barrelled countable enlargements and the bounding cardinal. J. London Math. Soc., to appear.Google Scholar
11.Saxon, S. A. and Ruiz, L. M. Sánchez, Barralled countable enlargements and the dominating cardinal. Preprint.Google Scholar
12.Tsirulnikov, B., On the locally convex noncomplete quasi-distinguished spaces. Bull. Soc1. Roy. Sci. Liège 47 (1978), 147–152.Google Scholar
13.Tweddle, I., Barrelled spaces whose bounded sets have at most countable dimension. J. London Math. Soc. (2) 29 (1984), 276–282.CrossRefGoogle Scholar
14.Tweddle, I., Saxon, S. A. and Ruiz, L. M. Sánchez, Barrelled countable enlargements, in Topological Vector Spaces, Algebras & Related Areas (eds. Lau, A. and Tweddle, I.) (Longman, 1994), 3–15.Google Scholar