Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-16T12:24:09.818Z Has data issue: false hasContentIssue false
  • English
  • Français

The range of non-surjective convolution operators on Beurling spaces

Published online by Cambridge University Press:  18 May 2009

José Bonet  and
Antonio Galbis
José Bonet
Affiliation:
Departamento de Matemática Aplicada, E.T.S. Arquitectura, Camino de Vera, E-46071 Valencia, Spain
Antonio Galbis
Affiliation:
Departamento de Análisis Matemático, Universidad de Valencia, Doctor Moliner 50, E-46100 Burjasot (Valencia), Spain
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let μ ≠ 0 be an ultradistribution of Beurling type with compact support in the space 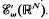. We investigate the range of the convolution operator Tμ on the space of non-quasianalytic functions of Beurling type 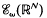associated with a weight w, in the case the operator is not surjective. It is proved that the range of TM always contains the space of real-analytic functions, and that it contains a smaller space of Beurling type 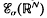for a weight σ ≥ ω if and only if the convolution operator is surjective on the smaller class.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 38 , Issue 1 , January 1996 , pp. 125 - 135
Copyright
Copyright © Glasgow Mathematical Journal Trust 1996

References

REFERENCES

1.Berenstein, C. A. and Taylor, B. A., Interpolation problems in CN with applications to harmonic analysis. J. d'Analyse Math. 38 (1980), 188–254.Google Scholar
2.Bonet, J., Meise, R. and Taylor, B. A., On the range of the Borel map for classes of non-quasianalytic functions, in: Progress in Functional Analysis, North Holland Math. Studies 170 (1992), 97–111.Google Scholar
3.Braun, R. W., Meise, R. and Taylor, B. A., Ultradifferentiable functions and Fourier analysis, Resultate Math. 17 (1990), 206–237.Google Scholar
4.Braun, R. W., Meise, R. and Vogt, D., Existence of fundamental solutions and surjectivity of convolution operators on classes of ultradifferentiable functions, Proc. London Math. Soc. (3) 61 (1990), 344–370.Google Scholar
5.Chou, Ch., La Transformation de Fourier Complexe et l'Équation de Convolution, Lecture Notes in Math. 325 (Springer Verlag, 1973).Google Scholar
6.Cioranescu, I., Convolution equations in w-ultradistribution spaces, Rev. Roum. Math. Pures et Appl. 25 (1980), 719–737.Google Scholar
7.Ehrenpreis, L., Solution to some problems of division, Part I. Amer. J. Math. 76 (1954), 883–903.CrossRefGoogle Scholar
8.Ehrenpreis, L., Solution to some problems of division, Part III. Amer. J. Math. 78 (1956), 685–715.CrossRefGoogle Scholar
9.Ehrenpreis, L., Solution of some problems of division, Part IV. Invertible and elliptic operators, Amer. J. Math. 82 (1960), 522–588.Google Scholar
10.Ehrenpreis, L. and Malliavin, P., Invertible operators and interpolation in AU spaces, J. Math. Pures Appl. 53 (1974), 165–182.Google Scholar
11.Floret, K., Some aspects of the theory of locally convex inductive limits, Functional Analysis: Surveys and Recent Results II, North-Holland Math. Studies 38 (1980), 205–237.Google Scholar
12.Grudzinski, O. V., Konstruktion von Fundamentallosungen für Convolutoren, Manuscripta Math. 19 (1976), 283–317.Google Scholar
13.Grudzinski, O. V., Examples of solvable and non-solvable convolution equations in K′p, p≥ 1, Pacific Journal Math. 80 (1979), 561–574.Google Scholar
14.Grudzinski, O. V., Slowly decreasing entire functions and convolution equations, Partial Differential Equations, Banach Center Publication 10 (1983), 169–184.Google Scholar
15.Hörmander, L., On the range of convolution operators, Ann. of Math. 76 (1962), 148–170.Google Scholar
16.Hörmander, L., An Introduction to Complex Analysis in Several Variables (Princeton University Press, 1967).Google Scholar
17.Hörmander, L., The Analysis of Linear Partial Differential Operators I (Springer, 1983).Google Scholar
18.Hörmander, L., The Analysis of Linear Partial Differential Operators II (Springer, 1983).Google Scholar
19.Kelleher, J. J. and Taylor, B. A., Closed ideals in locally convex algebras, J. reine angew. Math. 255 (1972), 190–209.Google Scholar
20.Malgrange, B., Existence et approximation des solutions des équations aux dérivées partielles et des équations de convolution, Ann. Inst. Fourier Grenoble 6 (1955–1956), 271–355.Google Scholar
21.Malgrange, B., Sur la propagation de la régularité des solutions des équations a coefficients constants, Bull. Math. Soc. Math. Phys. Roumanie 3 (53) (1959), 443–446.Google Scholar
22.Meise, R. and Taylor, B. A., Each non-zero convolution operator on the entire functions admits a continuous linear right inverse, Math. Z. 197 (1988), 139–152.CrossRefGoogle Scholar
23.Meise, R. and Taylor, B. A., Whitney's extension theorem for ultradifferentiable functions of Beurling type, Arkiv Mat. 26 (1988), 265–287.Google Scholar
24.Meise, R., Taylor, B. A. and Vogt, D., Equivalence of slowly decreasing conditions and local Fourier expansion, Indiana Univ. Math. J. 36 (1987), 729–756.Google Scholar
25.Momm, S., Closed ideals in nonradial Hörmander algebras, Archiv Math. 58 (1992), 47–55.Google Scholar
26.Momm, S., Division problems in spaces of entire functions of finite order, Functional Analysis (Ed. Bierstedt, K. D., Pietsch, A., Ruess, W., Vogt, D.) (Marcel Dekker, 1993), 435–457.Google Scholar
27.Momm, S., A Phragmen-Lindelöf theorem for plurisubharmonic functions on cones in CN, Indiana Univ. Math, J. 41 (1992) 861–867.CrossRefGoogle Scholar
28.Carreras, P. Pérez and Bonet, J., Barrelled Locally Convex Spaces, North-Holland Math. Studies 131 (1987).Google Scholar