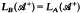Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-15T03:32:53.916Z Has data issue: false hasContentIssue false
  • English
  • Français

Ranges of Lyapunov Transformations for operator algebras

Published online by Cambridge University Press:  18 May 2009

J. Kyle
J. Kyle
Affiliation:
Department of Mathematics, University of Technology, Loughborough.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we shall extend results obtained in [5] to the W*-algebra setting.

Let 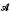be a C*-algebra and let 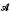+ denote the set of positive elements in 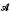. Given a fixed element A in 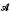, the Lyapunov transformation LA corresponding to A is the mapping of 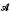into itself which sends X to AX+XA*. We are interested in characterizing those Bin 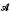for which

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 19 , Issue 2 , July 1978 , pp. 129 - 134
Copyright
Copyright © Glasgow Mathematical Journal Trust 1978

References

REFERENCES

1.Gleason, A. M., Projective topological spaces, Illinois J. Math. 2 (1958) 482–489.CrossRefGoogle Scholar
2.Glimm, J. G., A Stone-Weierstrass theorem for C*-algebras, Ann. of Math. 72 (1960) 216–244.CrossRefGoogle Scholar
3.Halpern, H., Irreducible module homomorphisms of a von Neumann algebra into its centre, Trans. Amer. Math. Soc. 140 (1969) 195–221.CrossRefGoogle Scholar
4.Kyle, J., Norms, spectra and numerical ranges of derivations, Ph.D thesis, University of Newcastle upon Tyne (1974).Google Scholar
5.Kyle, J., Ranges of Lyapunov transformations for Hilbert space, Glasgow Math. J. 19 (1978) 99–101.CrossRefGoogle Scholar
6.Loewy, R., On ranges of Lyapunov transformations IV, Glasgow Math. J., 17 (1976) 112–118.CrossRefGoogle Scholar
7.Loewy, R., On ranges of Lyapunov transformations III, SLAM J. Appl. Math., 30 (1976) 687–702.CrossRefGoogle Scholar
8.Takeda, Z., Conjugate spaces of operator algebras, Proc. Japan. Acad. 28 (1954) 90–95.Google Scholar