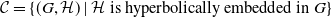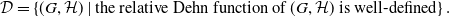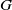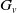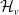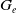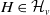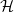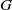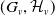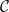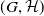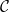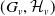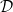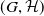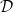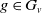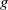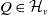1. Introduction
Consider the following classes of pairs consisting of a group and a finite collection of subgroups:
-
•
 $ \mathcal{C}= \left \{ (G,\mathcal{H}) \mid \text{$\mathcal{H}$ is hyperbolically embedded in $G$} \right \}$
$ \mathcal{C}= \left \{ (G,\mathcal{H}) \mid \text{$\mathcal{H}$ is hyperbolically embedded in $G$} \right \}$
-
•
 $ \mathcal{D}= \left \{ (G,\mathcal{H}) \mid \text{the relative Dehn function of $(G,\mathcal{H})$ is well-defined} \right \} .$
$ \mathcal{D}= \left \{ (G,\mathcal{H}) \mid \text{the relative Dehn function of $(G,\mathcal{H})$ is well-defined} \right \} .$
Theorem 1.1.
Let
![]() $G$
be a group that splits as a finite graph of groups such that each vertex group
$G$
be a group that splits as a finite graph of groups such that each vertex group
![]() $G_v$
is assigned a finite collection of subgroups
$G_v$
is assigned a finite collection of subgroups
![]() $\mathcal{H}_v$
, and each edge group
$\mathcal{H}_v$
, and each edge group
![]() $G_e$
is conjugate to a subgroup of some
$G_e$
is conjugate to a subgroup of some
![]() $H\in \mathcal{H}_v$
if
$H\in \mathcal{H}_v$
if
![]() $e$
is adjacent to
$e$
is adjacent to
![]() $v$
. Then there is a finite collection of subgroups
$v$
. Then there is a finite collection of subgroups
![]() $\mathcal{H}$
of
$\mathcal{H}$
of
![]() $G$
such that
$G$
such that
-
1. If each
 $(G_v, \mathcal{H}_v)$
is in
$(G_v, \mathcal{H}_v)$
is in
 $\mathcal C$
, then
$\mathcal C$
, then
 $(G,\mathcal{H})$
is in
$(G,\mathcal{H})$
is in
 $\mathcal C$
.
$\mathcal C$
. -
2. If each
 $(G_v, \mathcal{H}_v)$
is in
$(G_v, \mathcal{H}_v)$
is in
 $\mathcal D$
, then
$\mathcal D$
, then
 $(G,\mathcal{H})$
is in
$(G,\mathcal{H})$
is in
 $\mathcal D$
.
$\mathcal D$
. -
3. For any vertex
 $v$
and for any
$v$
and for any
 $g\in G_v$
, the element
$g\in G_v$
, the element
 $g$
is conjugate in
$g$
is conjugate in
 $G_v$
to an element of some
$G_v$
to an element of some
 $Q\in \mathcal{H}_v$
if and only if
$Q\in \mathcal{H}_v$
if and only if
 $g$
is conjugate in
$g$
is conjugate in
 $G$
to an element of some
$G$
to an element of some
 $H\in \mathcal{H}$
.
$H\in \mathcal{H}$
.
The theorem is trivial without the third item in the conclusion; indeed, the pair
![]() $(G, \{G\})$
belongs to both
$(G, \{G\})$
belongs to both
![]() $\mathcal{C}$
and
$\mathcal{C}$
and
![]() $\mathcal{D}$
. In comparison with previous results in the literature, our main contribution is that our combination results do not assume that edge groups are finitely generated or contained in
$\mathcal{D}$
. In comparison with previous results in the literature, our main contribution is that our combination results do not assume that edge groups are finitely generated or contained in
![]() $\mathcal{H}_v$
.
$\mathcal{H}_v$
.
The notion of a hyperbolically embedded collection of subgroups was introduced by Dahmani, Guirardel, and Osin [Reference Dahmani, Guirardel and Osin9]. A pair
![]() $(G,\mathcal{H})$
in
$(G,\mathcal{H})$
in
![]() $\mathcal{C}$
is called a hyperbolically embedded pair, and we write
$\mathcal{C}$
is called a hyperbolically embedded pair, and we write
![]() $\mathcal{H}\hookrightarrow _h G$
. Our combination results for hyperbolically embedded pairs
$\mathcal{H}\hookrightarrow _h G$
. Our combination results for hyperbolically embedded pairs
![]() $(G,\mathcal{H})$
generalize analogous results for relatively hyperbolic pairs in [Reference Alibegović1, Reference Bigdely and Wise7, Reference Dahmani8, Reference Mj and Reeves16, Reference Osin17] and for hyperbolically embedded pairs [Reference Dahmani, Guirardel and Osin9, Reference Minasyan and Osin14].
$(G,\mathcal{H})$
generalize analogous results for relatively hyperbolic pairs in [Reference Alibegović1, Reference Bigdely and Wise7, Reference Dahmani8, Reference Mj and Reeves16, Reference Osin17] and for hyperbolically embedded pairs [Reference Dahmani, Guirardel and Osin9, Reference Minasyan and Osin14].
The notions of finite relative presentation and relative Dehn function
![]() $\Delta _{G, \mathcal{H}}$
of a group
$\Delta _{G, \mathcal{H}}$
of a group
![]() $G$
with respect to a collection of subgroups
$G$
with respect to a collection of subgroups
![]() $\mathcal{H}$
were introduced by Osin [Reference Osin18] generalizing the notions of finite presentation and Dehn function of a group. A pair
$\mathcal{H}$
were introduced by Osin [Reference Osin18] generalizing the notions of finite presentation and Dehn function of a group. A pair
![]() $(G,\mathcal{H})$
is called finitely presented if
$(G,\mathcal{H})$
is called finitely presented if
![]() $G$
is finitely presented relative to
$G$
is finitely presented relative to
![]() $\mathcal{H}$
, and
$\mathcal{H}$
, and
![]() $\Delta _{G,\mathcal{H}}$
is called the Dehn function of the pair
$\Delta _{G,\mathcal{H}}$
is called the Dehn function of the pair
![]() $(G,\mathcal{H})$
. While a finitely presented group has a well-defined Dehn function; in contrast, the Dehn function of a finitely presented pair
$(G,\mathcal{H})$
. While a finitely presented group has a well-defined Dehn function; in contrast, the Dehn function of a finitely presented pair
![]() $(G,\mathcal{H})$
is not always well defined, for a characterization see [Reference Hughes, Martínez-Pedroza and Saldana12, Thm.E(2)]. Our result generalizes combination results for pairs
$(G,\mathcal{H})$
is not always well defined, for a characterization see [Reference Hughes, Martínez-Pedroza and Saldana12, Thm.E(2)]. Our result generalizes combination results for pairs
![]() $(G,\mathcal{H})$
with well-defined Dehn function by Osin [Reference Osin17, Thms. 1.2 and 1.3].
$(G,\mathcal{H})$
with well-defined Dehn function by Osin [Reference Osin17, Thms. 1.2 and 1.3].
We prove Theorem 1.1 for the case of graphs of groups with a single edge, since then the general case follows directly by induction on the number of edges of the graph. This particular case splits into three subcases corresponding to the three results stated below. The proofs of these subcases use characterizations of pairs
![]() $(G,\mathcal{H})$
being hyperbolically embedded [Reference Martínez-Pedroza and Rashid15, Thm. 5.9] and having a well defined Dehn function [Reference Hughes, Martínez-Pedroza and Saldana12, Thm. 4.7] in terms of existence of
$(G,\mathcal{H})$
being hyperbolically embedded [Reference Martínez-Pedroza and Rashid15, Thm. 5.9] and having a well defined Dehn function [Reference Hughes, Martínez-Pedroza and Saldana12, Thm. 4.7] in terms of existence of
![]() $G$
-graphs with certain properties that relate to Bowditch’s fineness [Reference Bowditch5]. These characterizations are discussed in Section 2. The proof of Theorem 1.1 for the case of a graph of groups with a single edge entails the construction of graphs satisfying the conditions of those characterizations for the fundamental group of the graph of groups. We use the existing graphs for the vertex groups as building blocks.
$G$
-graphs with certain properties that relate to Bowditch’s fineness [Reference Bowditch5]. These characterizations are discussed in Section 2. The proof of Theorem 1.1 for the case of a graph of groups with a single edge entails the construction of graphs satisfying the conditions of those characterizations for the fundamental group of the graph of groups. We use the existing graphs for the vertex groups as building blocks.
Our method of proof provides lower and upper bounds for the relative Dehn function of the fundamental group of the graph of groups in the terms of the relative Dehn functions of the vertex groups; see Section 6. Specifically, Theorem 1.6 below generalizes results of Brick [Reference Brick6] on bounds for the Dehn functions of free products (see the improvement by Guba and Sapir [Reference Guba and Sapir11]) and improve the bounds found by Osin for relative Dehn functions in [Reference Osin18, Thms 1.2 and 1.3].
Our main result reduces to the following statements.
Theorem 1.2 (Amalgamated Product). For
![]() $i\in \{ 1,2\}$
, let
$i\in \{ 1,2\}$
, let
![]() $(G_i, \mathcal{H}_i\cup \{K_i\})$
be a pair and
$(G_i, \mathcal{H}_i\cup \{K_i\})$
be a pair and
![]() $\partial _i\;:\; C\to K_i$
a group monomorphism. Let
$\partial _i\;:\; C\to K_i$
a group monomorphism. Let
![]() $G_1\ast _C G_2$
denote the amalgamated product determined by
$G_1\ast _C G_2$
denote the amalgamated product determined by
![]() $G_1\xleftarrow{\partial _1}C\xrightarrow{\partial _2}G_2$
, and let
$G_1\xleftarrow{\partial _1}C\xrightarrow{\partial _2}G_2$
, and let
![]() $\mathcal{H}=\mathcal{H}_1\cup \mathcal{H}_2$
. Then:
$\mathcal{H}=\mathcal{H}_1\cup \mathcal{H}_2$
. Then:
-
1. If
 $\mathcal{H}_i\cup \{K_i\} \hookrightarrow _h G_i$
for each
$\mathcal{H}_i\cup \{K_i\} \hookrightarrow _h G_i$
for each
 $i$
, then
$i$
, then
 $\mathcal{H}\cup \{\langle K_1,K_2\rangle \} \hookrightarrow _h G_1\ast _C G_2$
.
$\mathcal{H}\cup \{\langle K_1,K_2\rangle \} \hookrightarrow _h G_1\ast _C G_2$
. -
2. If
 $( G_i,\mathcal{H}_i\cup \{K_i\} ) \in \mathcal D$
for each
$( G_i,\mathcal{H}_i\cup \{K_i\} ) \in \mathcal D$
for each
 $i$
, then
$i$
, then
 $(G_1\ast _C G_2, \mathcal{H} \cup \{\langle K_1,K_2 \rangle \}) \in \mathcal D$
.
$(G_1\ast _C G_2, \mathcal{H} \cup \{\langle K_1,K_2 \rangle \}) \in \mathcal D$
. -
3. For any
 $g\in G_i$
, the element
$g\in G_i$
, the element
 $g$
is conjugate in
$g$
is conjugate in
 $G_i$
to an element of some
$G_i$
to an element of some
 $Q\in \mathcal{H}_i\cup \{K_i\}$
if and only if
$Q\in \mathcal{H}_i\cup \{K_i\}$
if and only if
 $g$
is conjugate in
$g$
is conjugate in
 $G$
to an element of some
$G$
to an element of some
 $H\in \mathcal{H}\cup \{ \langle K_1, K_2 \rangle \}$
.
$H\in \mathcal{H}\cup \{ \langle K_1, K_2 \rangle \}$
.
In the following statements, for a subgroup
![]() $K$
of a group
$K$
of a group
![]() $G$
and an element
$G$
and an element
![]() $g\in G$
, the conjugate subgroup
$g\in G$
, the conjugate subgroup
![]() $gKg^{-1}$
is denoted by
$gKg^{-1}$
is denoted by
![]() $K^g$
.
$K^g$
.
Theorem 1.3 (HNN-extension I). Let
![]() $(G, \mathcal{H} \cup \{K,L\})$
be a pair with
$(G, \mathcal{H} \cup \{K,L\})$
be a pair with
![]() $K\neq L$
,
$K\neq L$
,
![]() $C$
a subgroup of
$C$
a subgroup of
![]() $K$
, and
$K$
, and
![]() $\varphi \;:\; C\to L$
a group monomorphism. Let
$\varphi \;:\; C\to L$
a group monomorphism. Let
![]() $G\ast _{\varphi }$
denote the HNN-extension
$G\ast _{\varphi }$
denote the HNN-extension
![]() $\langle G, t\mid t c t^{-1} =\varphi (c) \text{ for all $c\in C$} \rangle$
. Then:
$\langle G, t\mid t c t^{-1} =\varphi (c) \text{ for all $c\in C$} \rangle$
. Then:
-
1. If
 $\mathcal{H} \cup \{K,L\}\hookrightarrow _h G$
then
$\mathcal{H} \cup \{K,L\}\hookrightarrow _h G$
then
 $\mathcal{H} \cup \{\langle K^t, L\rangle \} \hookrightarrow _h G\ast _{\varphi }$
.
$\mathcal{H} \cup \{\langle K^t, L\rangle \} \hookrightarrow _h G\ast _{\varphi }$
. -
2. If
 $(G, \mathcal{H}\cup \{K,L\}) \in \mathcal{D}$
, then
$(G, \mathcal{H}\cup \{K,L\}) \in \mathcal{D}$
, then
 $(G\ast _{\varphi },\mathcal{H} \cup \{\langle K^t, L\rangle \}) \in \mathcal D$
.
$(G\ast _{\varphi },\mathcal{H} \cup \{\langle K^t, L\rangle \}) \in \mathcal D$
. -
3. For any
 $g\in G$
, the element
$g\in G$
, the element
 $g$
is conjugate in
$g$
is conjugate in
 $G$
to an element of some
$G$
to an element of some
 $Q\in \mathcal{H} \cup \{K, L\}$
if and only if
$Q\in \mathcal{H} \cup \{K, L\}$
if and only if
 $g$
is conjugate in
$g$
is conjugate in
 $G\ast _\varphi$
to an element of some
$G\ast _\varphi$
to an element of some
 $H\in \mathcal{H}\cup \{ \langle K^t, L \rangle \}$
.
$H\in \mathcal{H}\cup \{ \langle K^t, L \rangle \}$
.
Note that the third items of Theorems 1.2 and 1.3 follow directly from standard arguments in combinatorial group theory. This article focuses on proving the other statements.
Corollary 1.4 (HNN-extension II). Let
![]() $(G, \mathcal{H} \cup \{K\})$
be a pair,
$(G, \mathcal{H} \cup \{K\})$
be a pair,
![]() $C$
a subgroup of
$C$
a subgroup of
![]() $K$
,
$K$
,
![]() $s\in G$
, and
$s\in G$
, and
![]() $\varphi \;:\; C\to K^s$
a group monomorphism. Let
$\varphi \;:\; C\to K^s$
a group monomorphism. Let
![]() $G\ast _{\varphi }$
denote the HNN-extension
$G\ast _{\varphi }$
denote the HNN-extension
![]() $\langle G, t\mid t c t^{-1} =\varphi (c) \text{ for all $c\in C$} \rangle$
. Then:
$\langle G, t\mid t c t^{-1} =\varphi (c) \text{ for all $c\in C$} \rangle$
. Then:
-
1. If
 $\mathcal{H} \cup \{K\}\hookrightarrow _h G$
then
$\mathcal{H} \cup \{K\}\hookrightarrow _h G$
then
 $\mathcal{H} \cup \{\langle K, s^{-1}t\rangle \} \hookrightarrow _h G\ast _{\varphi }$
.
$\mathcal{H} \cup \{\langle K, s^{-1}t\rangle \} \hookrightarrow _h G\ast _{\varphi }$
. -
2. If
 $(G, \mathcal{H}\cup \{K\}) \in \mathcal{D}$
, then
$(G, \mathcal{H}\cup \{K\}) \in \mathcal{D}$
, then
 $(G\ast _{\varphi },\mathcal{H} \cup \{\langle K, s^{-1}t\rangle \}) \in \mathcal D$
.
$(G\ast _{\varphi },\mathcal{H} \cup \{\langle K, s^{-1}t\rangle \}) \in \mathcal D$
. -
3. For any
 $g\in G$
, the element
$g\in G$
, the element
 $g$
is conjugate in
$g$
is conjugate in
 $G$
to an element of some
$G$
to an element of some
 $Q\in \mathcal{H} \cup \{K\}$
if and only if
$Q\in \mathcal{H} \cup \{K\}$
if and only if
 $g$
is conjugate in
$g$
is conjugate in
 $G\ast _\varphi$
to an element of some
$G\ast _\varphi$
to an element of some
 $H\in \mathcal{H}\cup \{ \langle K, s^{-1}t \rangle \}$
.
$H\in \mathcal{H}\cup \{ \langle K, s^{-1}t \rangle \}$
.
Proof. First, we prove the statement in the case that
![]() $s$
is the identity element of
$s$
is the identity element of
![]() $G$
. Let
$G$
. Let
![]() $L$
be the HNN-extension
$L$
be the HNN-extension
![]() $L=K\ast _\varphi$
. Observe that there is a natural isomorphism between
$L=K\ast _\varphi$
. Observe that there is a natural isomorphism between
![]() $G\ast _{\varphi }$
and the amalgamated product
$G\ast _{\varphi }$
and the amalgamated product
![]() $G\ast _{K} L$
. In this case, the conclusion of the corollary is obtained directly by invoking Theorem 1.2, since the pair
$G\ast _{K} L$
. In this case, the conclusion of the corollary is obtained directly by invoking Theorem 1.2, since the pair
![]() $(L, \{L\} )$
is in both classes
$(L, \{L\} )$
is in both classes
![]() $\mathcal C$
and
$\mathcal C$
and
![]() $\mathcal D$
.
$\mathcal D$
.
Now we argue in the case that
![]() $s\in G$
is arbitrary. Let
$s\in G$
is arbitrary. Let
![]() $\psi \;:\; C \to K$
the composition
$\psi \;:\; C \to K$
the composition
![]() $I_s\circ \varphi$
where
$I_s\circ \varphi$
where
![]() $I_s$
is the inner automorphism
$I_s$
is the inner automorphism
![]() $I_s(x)=s^{-1}xs$
. Since
$I_s(x)=s^{-1}xs$
. Since
there is a natural isomorphism
![]() $G\ast _\varphi \to G\ast _\psi$
which restricts to the identity on the base group
$G\ast _\varphi \to G\ast _\psi$
which restricts to the identity on the base group
![]() $G$
, and the stable letter of
$G$
, and the stable letter of
![]() $G\ast _\psi$
corresponds to
$G\ast _\psi$
corresponds to
![]() $s^{-1}t$
in
$s^{-1}t$
in
![]() $G\ast _\varphi$
. Since
$G\ast _\varphi$
. Since
![]() $\psi$
maps
$\psi$
maps
![]() $C\leq K$
into
$C\leq K$
into
![]() $K$
, we have reduced the case of arbitrary
$K$
, we have reduced the case of arbitrary
![]() $s\in G$
to the case that
$s\in G$
to the case that
![]() $s$
is the identity in
$s$
is the identity in
![]() $G$
and the statement of the corollary follows.
$G$
and the statement of the corollary follows.
Let us describe the argument proving our main result using the three previous statements. The argument relies on the following observation.
Remark 1.5.
If a pair
![]() $(G,\mathcal{H}\cup \{L\})$
belongs to
$(G,\mathcal{H}\cup \{L\})$
belongs to
![]() $\mathcal C$
(respectively
$\mathcal C$
(respectively
![]() $\mathcal D$
) and
$\mathcal D$
) and
![]() $g\in G$
then
$g\in G$
then
![]() $(G,\mathcal{H}\cup \{L^g\})$
belongs to
$(G,\mathcal{H}\cup \{L^g\})$
belongs to
![]() $\mathcal C$
(respectively
$\mathcal C$
(respectively
![]() $\mathcal D$
). This statement can be seen directly from the original definitions of hyperbolically embedded collection of subgroups [Reference Dahmani, Guirardel and Osin9] and relative Dehn function [Reference Osin18]. It can be also deduced directly from Theorems 2.2 and 2.9, respectively, in the main body of the article.
$\mathcal D$
). This statement can be seen directly from the original definitions of hyperbolically embedded collection of subgroups [Reference Dahmani, Guirardel and Osin9] and relative Dehn function [Reference Osin18]. It can be also deduced directly from Theorems 2.2 and 2.9, respectively, in the main body of the article.
Proof of Theorem 1.1. The case of a tree of groups satisfying the hypothesis of the theorem follows from Theorem 1.2 and Remark 1.5. Then the general case reduces to the case of a graph of groups with a single vertex, where the vertex group corresponds to the fundamental group of a maximal tree of groups. In the case of a graph of groups with a single vertex, each edge corresponds to applying either Theorem 1.3 or Corollary 1.4 together with Remark 1.5.
The following theorem generalizes results of Brick [Reference Brick6, Proposition 3.2] on bounds on Dehn functions of free products and improve bounds for relative Dehn functions found by Osin [Reference Osin18, Theorems 1.2 and 1.3].
Theorem 1.6.
-
1. Under the assumptions of Theorem 1.2 (2), if
 $\Delta$
is a relative Dehn function of
$\Delta$
is a relative Dehn function of
 $(G_1\ast _C G_2, \mathcal{H} \cup \{\langle K_1,K_2 \rangle \})$
and
$(G_1\ast _C G_2, \mathcal{H} \cup \{\langle K_1,K_2 \rangle \})$
and
 $\Delta _i$
is a relative Dehn function of
$\Delta _i$
is a relative Dehn function of
 $(G_i, \mathcal{H}_i \cup \{K_i\})$
then
where
$(G_i, \mathcal{H}_i \cup \{K_i\})$
then
where \begin{equation*} \max \{\Delta _1,\Delta _2\} \preceq \Delta \preceq \max \left \{\overline {\Delta _1}, \overline {\Delta _2} \right \},\end{equation*}
\begin{equation*} \max \{\Delta _1,\Delta _2\} \preceq \Delta \preceq \max \left \{\overline {\Delta _1}, \overline {\Delta _2} \right \},\end{equation*}
 $\overline{\Delta _i}$
denotes the super-additive closure of
$\overline{\Delta _i}$
denotes the super-additive closure of
 $\Delta _i$
.
$\Delta _i$
.
-
2. Under the assumptions of Theorem 1.3(2), if
 $\Delta$
is a relative Dehn function of
$\Delta$
is a relative Dehn function of
 $(G\ast _\varphi, \mathcal{H} \cup \{\langle K^t,L \rangle \})$
and
$(G\ast _\varphi, \mathcal{H} \cup \{\langle K^t,L \rangle \})$
and
 $\Delta _0$
is a relative Dehn function of
$\Delta _0$
is a relative Dehn function of
 $(G, \mathcal{H} \cup \{K, L\})$
then
where
$(G, \mathcal{H} \cup \{K, L\})$
then
where \begin{equation*} \Delta _0 \preceq \Delta \preceq \overline {\Delta _0 },\end{equation*}
\begin{equation*} \Delta _0 \preceq \Delta \preceq \overline {\Delta _0 },\end{equation*}
 $\overline{\Delta _0}$
is the super-additive closure of
$\overline{\Delta _0}$
is the super-additive closure of
 $\Delta _0$
$\Delta _0$
-
3. Under the assumptions of Corollary 1.4(2), if
 $\Delta$
is a relative Dehn function of
$\Delta$
is a relative Dehn function of
 $(G\ast _{\varphi },\mathcal{H} \cup \{\langle K, s^{-1}t\rangle \})$
and
$(G\ast _{\varphi },\mathcal{H} \cup \{\langle K, s^{-1}t\rangle \})$
and
 $\Delta _0$
is a relative Dehn function of
$\Delta _0$
is a relative Dehn function of
 $(G, \mathcal{H}\cup \{K\})$
then
where
$(G, \mathcal{H}\cup \{K\})$
then
where \begin{equation*} \Delta _0 \preceq \Delta \preceq \overline {\Delta _0},\end{equation*}
\begin{equation*} \Delta _0 \preceq \Delta \preceq \overline {\Delta _0},\end{equation*}
 $\overline{\Delta _0}$
is the super-additive closure of
$\overline{\Delta _0}$
is the super-additive closure of
 $\Delta _0$
$\Delta _0$
We conclude the introduction with a more detailed comparison of our results with previous results in the literature.
-
1. Dahmani, Guirardel, and Osin proved Theorem 1.2(1) in the case that
 $\partial _1\;:\; C\to K_1$
is an isomorphism and
$\partial _1\;:\; C\to K_1$
is an isomorphism and
 $K_1$
is finitely generated [Reference Dahmani, Guirardel and Osin9, Thm 6.20]; and Theorem 1.3(1) in the case that
$K_1$
is finitely generated [Reference Dahmani, Guirardel and Osin9, Thm 6.20]; and Theorem 1.3(1) in the case that
 $C=K$
and
$C=K$
and
 $K$
is finitely generated [Reference Dahmani, Guirardel and Osin9, Thm 6.19].
$K$
is finitely generated [Reference Dahmani, Guirardel and Osin9, Thm 6.19]. -
2. Osin proved Theorem 1.2(2) in the case that
 $\partial _1\;:\; C\to K_1$
is an isomorphism and
$\partial _1\;:\; C\to K_1$
is an isomorphism and
 $K_1$
is finitely generated, see [Reference Osin17, Thm 1.3]; and Theorem 1.3(2) in the case that
$K_1$
is finitely generated, see [Reference Osin17, Thm 1.3]; and Theorem 1.3(2) in the case that
 $C=K$
and
$C=K$
and
 $K$
is finitely generated, see [Reference Osin17, Thm 1.2].
$K$
is finitely generated, see [Reference Osin17, Thm 1.2]. -
3. Under the assumptions of Theorem 1.1, if each
 $(G_v, \mathcal{H}_v)\in \mathcal C$
for every vertex
$(G_v, \mathcal{H}_v)\in \mathcal C$
for every vertex
 $v$
, and there is at least one
$v$
, and there is at least one
 $v$
such that
$v$
such that
 $\mathcal{H}_v$
is nontrivial in
$\mathcal{H}_v$
is nontrivial in
 $G_v$
, the existence of a nontrivial collection
$G_v$
, the existence of a nontrivial collection
 $\mathcal{H}$
such that
$\mathcal{H}$
such that
 $(G, \mathcal{H})\in \mathcal{C}$
follows from results of Minasyan and Osin [Reference Minasyan and Osin14, Cor. 2.2 and 2.3] and the characterization of acylindrical hyperbolicity in terms of existence of proper infinite hyperbolically embedded subgroups by Osin [Reference Osin19]; by a nontrivial collection we mean that it contains a proper infinite subgroup. This alternative approach does not guarantee that the collection
$(G, \mathcal{H})\in \mathcal{C}$
follows from results of Minasyan and Osin [Reference Minasyan and Osin14, Cor. 2.2 and 2.3] and the characterization of acylindrical hyperbolicity in terms of existence of proper infinite hyperbolically embedded subgroups by Osin [Reference Osin19]; by a nontrivial collection we mean that it contains a proper infinite subgroup. This alternative approach does not guarantee that the collection
 $\mathcal{H}$
satisfies the third condition of Theorem 1.1.
$\mathcal{H}$
satisfies the third condition of Theorem 1.1. -
4. Theorems 1.2(1) and 1.3(1), in the case that
 $G_i$
is hyperbolic relative to
$G_i$
is hyperbolic relative to
 $\mathcal{H}_i$
for
$\mathcal{H}_i$
for
 $i=1,2$
, follow from results of Wise and the first author [Reference Bigdely and Wise7, Thm. A].
$i=1,2$
, follow from results of Wise and the first author [Reference Bigdely and Wise7, Thm. A].
1.1. Organization
The rest of the article consists of five sections. In Section 2, we review characterizations of pairs
![]() $(G, \mathcal{H})$
being hyperbolically embedded and having well-defined Dehn functions in terms of actions on graphs. In Section 3, we reduce the proof of Theorems 1.2 and 1.3 to prove two technical results, Theorems 3.1 and 3.2. Their proofs are the content of Sections 4 and 5, respectively. The last section contains the proof of Theorem 1.6.
$(G, \mathcal{H})$
being hyperbolically embedded and having well-defined Dehn functions in terms of actions on graphs. In Section 3, we reduce the proof of Theorems 1.2 and 1.3 to prove two technical results, Theorems 3.1 and 3.2. Their proofs are the content of Sections 4 and 5, respectively. The last section contains the proof of Theorem 1.6.
2. Characterizations using fineness
In this section, we describe a characterization of pairs
![]() $(G,\mathcal{H})$
being hyperbolically embedded, Theorem 2.2; and a characterization of the pairs having a well-defined Dehn function, Theorem 2.9. These characterizations are in terms of existence of
$(G,\mathcal{H})$
being hyperbolically embedded, Theorem 2.2; and a characterization of the pairs having a well-defined Dehn function, Theorem 2.9. These characterizations are in terms of existence of
![]() $G$
-graphs with certain properties that relate to Bowditch’s fineness [Reference Bowditch5], a notion that is defined below. The characterizations are re-statements of previous results in the literature [Reference Martínez-Pedroza and Rashid15, Thm. 5.9] and [Reference Hughes, Martínez-Pedroza and Saldana12, Thm. 4.7]. This section also includes a couple of lemmas that will be of use in later sections.
$G$
-graphs with certain properties that relate to Bowditch’s fineness [Reference Bowditch5], a notion that is defined below. The characterizations are re-statements of previous results in the literature [Reference Martínez-Pedroza and Rashid15, Thm. 5.9] and [Reference Hughes, Martínez-Pedroza and Saldana12, Thm. 4.7]. This section also includes a couple of lemmas that will be of use in later sections.
All graphs
![]() $\Gamma =(V,E)$
considered in this section are simplicial, so we consider the set of edges
$\Gamma =(V,E)$
considered in this section are simplicial, so we consider the set of edges
![]() $E$
to be a collection of subsets of cardinality two of the vertex set
$E$
to be a collection of subsets of cardinality two of the vertex set
![]() $V$
.
$V$
.
Let
![]() $\Gamma$
be a simplicial graph, let
$\Gamma$
be a simplicial graph, let
![]() $v$
be a vertex of
$v$
be a vertex of
![]() $\Gamma$
, and let
$\Gamma$
, and let
![]() $T_v\Gamma$
denote the set of the vertices adjacent to
$T_v\Gamma$
denote the set of the vertices adjacent to
![]() $v$
. For
$v$
. For
![]() $x, y \in T_v\Gamma$
, the angle metric
$x, y \in T_v\Gamma$
, the angle metric
![]() $\angle _v(x, y)$
is the combinatorial length of the shortest path in the graph
$\angle _v(x, y)$
is the combinatorial length of the shortest path in the graph
![]() $\Gamma -\{v\}$
between
$\Gamma -\{v\}$
between
![]() $x$
and
$x$
and
![]() $y$
, with
$y$
, with
![]() $\angle _v(x, y)=\infty$
if there is no such path. The graph
$\angle _v(x, y)=\infty$
if there is no such path. The graph
![]() $\Gamma$
is fine at
$\Gamma$
is fine at
![]() $v$
if
$v$
if
![]() $(T_v\Gamma, \angle _v)$
is a locally finite metric space. A graph is fine if it is fine at every vertex.
$(T_v\Gamma, \angle _v)$
is a locally finite metric space. A graph is fine if it is fine at every vertex.
It is an observation that a graph
![]() $\Gamma$
is fine if and only if for every pair of vertices
$\Gamma$
is fine if and only if for every pair of vertices
![]() $x,y$
and every positive integer
$x,y$
and every positive integer
![]() $n$
, there are finitely many embedded paths between
$n$
, there are finitely many embedded paths between
![]() $x$
and
$x$
and
![]() $y$
of length at most
$y$
of length at most
![]() $n$
; for a proof see [Reference Bowditch5].
$n$
; for a proof see [Reference Bowditch5].
2.1. Hyperbolically embedded pairs
In [Reference Osin19, Definition 2.9], Osin defines the notion of a collection of subgroups
![]() $\mathcal{H}$
being hyperbolically embedded into a group
$\mathcal{H}$
being hyperbolically embedded into a group
![]() $G$
. This relation is denoted as
$G$
. This relation is denoted as
![]() $\mathcal{H} \hookrightarrow _h G$
and, in this case, we say that the pair
$\mathcal{H} \hookrightarrow _h G$
and, in this case, we say that the pair
![]() $(G,\mathcal{H})$
is a hyperbolically embedded pair. In this article, we use the following characterization of hyperbolically embedded collection proved in [Reference Martínez-Pedroza and Rashid15] as our working definition.
$(G,\mathcal{H})$
is a hyperbolically embedded pair. In this article, we use the following characterization of hyperbolically embedded collection proved in [Reference Martínez-Pedroza and Rashid15] as our working definition.
Definition 2.1 (Proper pair). A pair
![]() $(G,\mathcal{H})$
is proper if
$(G,\mathcal{H})$
is proper if
![]() $\mathcal{H}$
is a finite collection of subgroups such that no two distinct infinite subgroups are conjugate in
$\mathcal{H}$
is a finite collection of subgroups such that no two distinct infinite subgroups are conjugate in
![]() $G$
.
$G$
.
Theorem 2.2 (Criterion for hyperbolically embedded pairs). [Reference Martínez-Pedroza and Rashid15, Theorem 5.9] A proper pair
![]() $(G,\mathcal{H})$
is a hyperbolically embedded pair if and only if there is a connected
$(G,\mathcal{H})$
is a hyperbolically embedded pair if and only if there is a connected
![]() $G$
-graph
$G$
-graph
![]() $\Gamma$
such that
$\Gamma$
such that
-
1. There are finitely many
 $G$
-orbits of vertices.
$G$
-orbits of vertices.
-
2. Edge
 $G$
-stabilizers are finite.
$G$
-stabilizers are finite.
-
3. Vertex
 $G$
-stabilizers are either finite or conjugates of subgroups in
$G$
-stabilizers are either finite or conjugates of subgroups in
 $\mathcal{H}$
.
$\mathcal{H}$
. -
4. Every
 $H\in \mathcal{H}$
is the
$H\in \mathcal{H}$
is the
 $G$
-stabilizer of a vertex of
$G$
-stabilizer of a vertex of
 $\Gamma$
.
$\Gamma$
. -
5.
 $\Gamma$
is hyperbolic.
$\Gamma$
is hyperbolic.
-
6.
 $\Gamma$
is fine at
$\Gamma$
is fine at
 $V_{\infty }(\Gamma )=\{v\in V(\Gamma ) | v \text{ has infinite stabilizer}\}$
.
$V_{\infty }(\Gamma )=\{v\in V(\Gamma ) | v \text{ has infinite stabilizer}\}$
.
Definition 2.3.
We refer to a graph
![]() $\Gamma$
satisfying the conditions of Theorem 2.2 as a
$\Gamma$
satisfying the conditions of Theorem 2.2 as a
![]() $(G, \mathcal{H})$
-graph
$(G, \mathcal{H})$
-graph
Let us observe that in [Reference Martínez-Pedroza and Rashid15], Theorem 2.2 is proved for the case that
![]() $\mathcal{H}$
consists of a single infinite subgroup, and the authors observe that the argument in the case that
$\mathcal{H}$
consists of a single infinite subgroup, and the authors observe that the argument in the case that
![]() $\mathcal{H}$
is a finite collection of infinite subgroups (such that no pair of distinct infinite subgroups in
$\mathcal{H}$
is a finite collection of infinite subgroups (such that no pair of distinct infinite subgroups in
![]() $\mathcal{H}$
are conjugate in
$\mathcal{H}$
are conjugate in
![]() $G$
) follows by the same argument. Then the general case in which
$G$
) follows by the same argument. Then the general case in which
![]() $\mathcal{H}$
is a finite collection of subgroups follows from the following statement: if
$\mathcal{H}$
is a finite collection of subgroups follows from the following statement: if
![]() $\mathcal{H}$
is a collection of subgroups and
$\mathcal{H}$
is a collection of subgroups and
![]() $K$
a finite subgroup of a group
$K$
a finite subgroup of a group
![]() $G$
, then:
$G$
, then:
-
1.
 $\mathcal{H}\hookrightarrow _h G$
if and only if
$\mathcal{H}\hookrightarrow _h G$
if and only if
 $\mathcal{H}\cup \{K\} \hookrightarrow _h G$
.
$\mathcal{H}\cup \{K\} \hookrightarrow _h G$
. -
2. There is
 $(G,\mathcal{H})$
-graph if and only if there is a
$(G,\mathcal{H})$
-graph if and only if there is a
 $(G,\mathcal{H}\cup \{K\})$
-graph.
$(G,\mathcal{H}\cup \{K\})$
-graph.
The first statement is a direct consequence of the definition of hyperbolically embedded collection by Osin [Reference Osin19]. The if part of the second statement is trivial, and the only if part follows directly from [Reference Arora and Martínez-Pedroza2, Thm. 3.4].
2.2. Relative presentations
In [Reference Osin18, Chapter 2], Osin introduces the notions of relative presentation of a group with respect to a collection of subgroups, and relative Dehn functions. We briefly recall these notions below.
Let
![]() $G$
be a group and let
$G$
be a group and let
![]() $\mathcal{H}$
be a collection of subgroups. A subset
$\mathcal{H}$
be a collection of subgroups. A subset
![]() $S$
of
$S$
of
![]() $G$
is a relative generating set of
$G$
is a relative generating set of
![]() $G$
with respect to
$G$
with respect to
![]() $\mathcal{H}$
if the natural homomorphism
$\mathcal{H}$
if the natural homomorphism
is surjective, where
![]() $F(S)$
denotes the free group with free generating set
$F(S)$
denotes the free group with free generating set
![]() $S$
. A relative generating set of
$S$
. A relative generating set of
![]() $G$
with respect to
$G$
with respect to
![]() $\mathcal{H}$
is called a generating set of the pair
$\mathcal{H}$
is called a generating set of the pair
![]() $(G, \mathcal{H})$
. A pair that admits a finite generating set is called a finitely generated pair. Let
$(G, \mathcal{H})$
. A pair that admits a finite generating set is called a finitely generated pair. Let
![]() $R\subseteq F(S,\mathcal{H})$
be a subset that normally generates the kernel of the above homomorphism. In this case, we have a short exact sequence of groups
$R\subseteq F(S,\mathcal{H})$
be a subset that normally generates the kernel of the above homomorphism. In this case, we have a short exact sequence of groups
and the triple
is called a relative presentation of
![]() $G$
with respect to
$G$
with respect to
![]() $\mathcal{H}$
, or just a presentation of the pair
$\mathcal{H}$
, or just a presentation of the pair
![]() $(G,\mathcal{H})$
. Abusing notation, we write
$(G,\mathcal{H})$
. Abusing notation, we write
![]() $G=\langle S, \mathcal{H}\mid R \rangle$
. If both
$G=\langle S, \mathcal{H}\mid R \rangle$
. If both
![]() $S$
and
$S$
and
![]() $R$
are finite we say that the pair
$R$
are finite we say that the pair
![]() $(G,\mathcal{H})$
is finitely presented.
$(G,\mathcal{H})$
is finitely presented.
Lemma 2.4.
Let
![]() $G$
be a group and let
$G$
be a group and let
![]() $\mathcal{H}_0\sqcup \mathcal{H}$
be a collection of subgroups. Let
$\mathcal{H}_0\sqcup \mathcal{H}$
be a collection of subgroups. Let
![]() $P$
denote the subgroup of
$P$
denote the subgroup of
![]() $G$
generated by
$G$
generated by
![]() $S_0$
and the subgroups in
$S_0$
and the subgroups in
![]() $\mathcal{H}_0$
. If
$\mathcal{H}_0$
. If
then
where
![]() $R'$
is the image of
$R'$
is the image of
![]() $R$
under the natural epimorphism
$R$
under the natural epimorphism
![]() $\varphi \;:\; F(S_0\cup S, \mathcal{H}_0\cup \mathcal{H}) \to F(S,\mathcal{H}\cup \{ P\})$
.
$\varphi \;:\; F(S_0\cup S, \mathcal{H}_0\cup \mathcal{H}) \to F(S,\mathcal{H}\cup \{ P\})$
.
Proof. Let
![]() $A=F(S, \mathcal{H})$
,
$A=F(S, \mathcal{H})$
,
![]() $B=F(S_0, \mathcal{H}_0)$
,
$B=F(S_0, \mathcal{H}_0)$
,
![]() $K$
the normal subgroup of
$K$
the normal subgroup of
![]() $B$
generated by
$B$
generated by
![]() $R_0$
and
$R_0$
and
![]() $N$
the normal subgroup of
$N$
the normal subgroup of
![]() $A\ast B=F(S_0\cup S, \mathcal{H}_0\cup \mathcal{H})$
generated by
$A\ast B=F(S_0\cup S, \mathcal{H}_0\cup \mathcal{H})$
generated by
![]() $R$
. Our hypotheses imply that the natural epimorphisms
$R$
. Our hypotheses imply that the natural epimorphisms
![]() $A\ast B \to G$
and
$A\ast B \to G$
and
![]() $B\to P$
induce short exact sequences:
$B\to P$
induce short exact sequences:
Let us identify
![]() $P=B/K$
. The natural epimorphism of the statement of the lemma
$P=B/K$
. The natural epimorphism of the statement of the lemma
induces an isomorphism:
By the definition of
![]() $N$
, we have that
$N$
, we have that
![]() $\varphi (N)$
is the normal subgroup of
$\varphi (N)$
is the normal subgroup of
![]() $A\ast P$
generated by
$A\ast P$
generated by
![]() $R'=\varphi (R)$
. Therefore, the natural epimorphism
$R'=\varphi (R)$
. Therefore, the natural epimorphism
![]() $A\ast P \to G$
induces a short exact sequence:
$A\ast P \to G$
induces a short exact sequence:
which concludes the proof.
The following pair of lemmas allow us to conclude that certain amalgamated products and HNN-extensions preserve relative finite presentability.
Lemma 2.5 (Amalgamated products). For
![]() $i\in \{ 1,2\}$
, let
$i\in \{ 1,2\}$
, let
![]() $(G_i, \mathcal{H}_i\cup \{K_i\})$
be a pair,
$(G_i, \mathcal{H}_i\cup \{K_i\})$
be a pair,
![]() $\partial _i\;:\; C\to K_i$
a group monomorphism. Let
$\partial _i\;:\; C\to K_i$
a group monomorphism. Let
![]() $G_1\ast _C G_2$
denote the amalgamated product determined by
$G_1\ast _C G_2$
denote the amalgamated product determined by
![]() $G_1\xleftarrow{\partial _1}C\xrightarrow{\partial _2}G_2$
, and
$G_1\xleftarrow{\partial _1}C\xrightarrow{\partial _2}G_2$
, and
![]() $\mathcal{H}=\mathcal{H}_1\cup \mathcal{H}_2$
. If
$\mathcal{H}=\mathcal{H}_1\cup \mathcal{H}_2$
. If
then
Proof. Observe that
![]() $\langle S_1\cup S_2, \mathcal{H}\cup \{K_1, K_2\} \mid R_1\cup R_2, \partial _1(c)=\partial _2(c) \text{ for all $c\in C$} \rangle$
is a relative presentation of
$\langle S_1\cup S_2, \mathcal{H}\cup \{K_1, K_2\} \mid R_1\cup R_2, \partial _1(c)=\partial _2(c) \text{ for all $c\in C$} \rangle$
is a relative presentation of
![]() $G_1\ast _C G_2$
. Since the subgroup
$G_1\ast _C G_2$
. Since the subgroup
![]() $\langle K_1, K_2 \rangle \leq G_1\ast _C G_2$
is isomorphic to the amalgamated product
$\langle K_1, K_2 \rangle \leq G_1\ast _C G_2$
is isomorphic to the amalgamated product
![]() $K_1\ast _C K_2$
, we have that
$K_1\ast _C K_2$
, we have that
![]() $\langle K_1,K_2 \mid \partial _1(c)=\partial _2(c) \text{ for all $c\in C$} \rangle$
is a relative presentation of
$\langle K_1,K_2 \mid \partial _1(c)=\partial _2(c) \text{ for all $c\in C$} \rangle$
is a relative presentation of
![]() $\langle K_1,K_2 \rangle$
. The proof concludes by invoking Lemma 2.4.
$\langle K_1,K_2 \rangle$
. The proof concludes by invoking Lemma 2.4.
Lemma 2.6 (HNN-extension). Let
![]() $(G, \mathcal{H} \cup \{K,L\})$
be a pair with
$(G, \mathcal{H} \cup \{K,L\})$
be a pair with
![]() $K\neq L$
,
$K\neq L$
,
![]() $C$
a subgroup of
$C$
a subgroup of
![]() $K$
,
$K$
,
![]() $\varphi \;:\; C\to L$
a group monomorphism, and let
$\varphi \;:\; C\to L$
a group monomorphism, and let
![]() $G\ast _{\varphi }$
denote the HNN-extension
$G\ast _{\varphi }$
denote the HNN-extension
![]() $\langle G, t\mid t c t^{-1} =\varphi (c) \text{for all $c\in C$} \rangle$
. If
$\langle G, t\mid t c t^{-1} =\varphi (c) \text{for all $c\in C$} \rangle$
. If
then
where
![]() $R'$
is the set of relations obtained by taking each element of
$R'$
is the set of relations obtained by taking each element of
![]() $R$
and replacing all occurrences of elements
$R$
and replacing all occurrences of elements
![]() $k\in K$
by words
$k\in K$
by words
![]() $t^{-1} k^t t$
. In particular,
$t^{-1} k^t t$
. In particular,
![]() $R$
and
$R$
and
![]() $R'$
have the same cardinality.
$R'$
have the same cardinality.
Proof. Let
![]() $J$
denote the subgroup
$J$
denote the subgroup
![]() $K^t$
, and let
$K^t$
, and let
![]() $\psi \;:\; K \to J$
be the isomorphism
$\psi \;:\; K \to J$
be the isomorphism
![]() $\psi (k)=tkt^{-1}$
. Observe that
$\psi (k)=tkt^{-1}$
. Observe that
![]() $\langle S, t, \mathcal{H}\cup \{K,L\} \mid R,\ tct^{-1}=\varphi (c) \text{ for all $c\in C$} \rangle$
is a presentation for the pair
$\langle S, t, \mathcal{H}\cup \{K,L\} \mid R,\ tct^{-1}=\varphi (c) \text{ for all $c\in C$} \rangle$
is a presentation for the pair
![]() $(G\ast _\varphi, \mathcal{H}\cup \{K,L\})$
. Therefore,
$(G\ast _\varphi, \mathcal{H}\cup \{K,L\})$
. Therefore,
A consequence of Britton’s lemma is that the subgroup
![]() $\langle J, L \rangle \leq G\ast _\varphi$
is isomorphic to the amalgamated product
$\langle J, L \rangle \leq G\ast _\varphi$
is isomorphic to the amalgamated product
![]() $J\ast _{\varphi (C)}L$
. Hence,
$J\ast _{\varphi (C)}L$
. Hence,
The proof concludes by invoking Lemma 2.4.
2.3. Relative Dehn functions
Suppose that
![]() $\langle S,\mathcal{H}\mid R\rangle$
is a finite relative presentation of the pair
$\langle S,\mathcal{H}\mid R\rangle$
is a finite relative presentation of the pair
![]() $(G,\mathcal{H})$
. For a word
$(G,\mathcal{H})$
. For a word
![]() $W$
over the alphabet
$W$
over the alphabet
![]() $\mathcal{S}=S\sqcup \bigsqcup _{H\in \mathcal{H}}(H-\{1\})$
representing the trivial element in
$\mathcal{S}=S\sqcup \bigsqcup _{H\in \mathcal{H}}(H-\{1\})$
representing the trivial element in
![]() $G$
, there is an expression:
$G$
, there is an expression:
where
![]() $R_i\in R$
and
$R_i\in R$
and
![]() $f_i\in F(S)$
. We say a function
$f_i\in F(S)$
. We say a function
![]() $f\;:\; \mathbb{N}\to \mathbb{N}$
is a relative isoperimetric function of the relative presentation
$f\;:\; \mathbb{N}\to \mathbb{N}$
is a relative isoperimetric function of the relative presentation
![]() $\langle S,\mathcal{H}\ |\ R \rangle$
if, for any
$\langle S,\mathcal{H}\ |\ R \rangle$
if, for any
![]() $n\in \mathbb{N}$
, and any word
$n\in \mathbb{N}$
, and any word
![]() $W$
over the alphabet
$W$
over the alphabet
![]() $\mathcal{S}$
of length
$\mathcal{S}$
of length
![]() $\leq n$
representing the trivial element in
$\leq n$
representing the trivial element in
![]() $G$
, one can write
$G$
, one can write
![]() $W$
as in (3) with
$W$
as in (3) with
![]() $k\leq f(n)$
. The smallest relative isoperimetric function of a finite relative presentation
$k\leq f(n)$
. The smallest relative isoperimetric function of a finite relative presentation
![]() $\langle S,\mathcal{H}\ |\ R \rangle$
is called the relative Dehn function of
$\langle S,\mathcal{H}\ |\ R \rangle$
is called the relative Dehn function of
![]() $G$
with respect to
$G$
with respect to
![]() $\mathcal{H}$
, or the Dehn function of the pair
$\mathcal{H}$
, or the Dehn function of the pair
![]() $(G, \mathcal{H})$
. This function is denoted by
$(G, \mathcal{H})$
. This function is denoted by
![]() $\Delta _{G,\mathcal{H}}$
. Theorem 2.7 below justifies the notation
$\Delta _{G,\mathcal{H}}$
. Theorem 2.7 below justifies the notation
![]() $\Delta _{G,\mathcal{H}}$
for the Dehn function of a finitely presented pair
$\Delta _{G,\mathcal{H}}$
for the Dehn function of a finitely presented pair
![]() $(G,\mathcal{H})$
.
$(G,\mathcal{H})$
.
For functions
![]() $f,g\;:\; \mathbb{N}\to \mathbb{N}$
, we write
$f,g\;:\; \mathbb{N}\to \mathbb{N}$
, we write
![]() $f\preceq g$
if there exist constants
$f\preceq g$
if there exist constants
![]() $C,K,L\in \mathbb{N}$
such that
$C,K,L\in \mathbb{N}$
such that
![]() $f(n)\leq Cg(Kn)+Ln$
for every
$f(n)\leq Cg(Kn)+Ln$
for every
![]() $n$
. We say
$n$
. We say
![]() $f$
and
$f$
and
![]() $g$
are asymptotically equivalent, denoted as
$g$
are asymptotically equivalent, denoted as
![]() $f \asymp g$
, if
$f \asymp g$
, if
![]() $f\preceq g$
and
$f\preceq g$
and
![]() $g\preceq f$
.
$g\preceq f$
.
Theorem 2.7. [Reference Osin18, Theorem 2.34] Let
![]() $G$
be a finitely presented group relative to the collection of subgroups
$G$
be a finitely presented group relative to the collection of subgroups
![]() $\mathcal{H}$
. Let
$\mathcal{H}$
. Let
![]() $\Delta _1$
and
$\Delta _1$
and
![]() $\Delta _2$
be the relative Dehn functions associated with two finite relative presentations. If
$\Delta _2$
be the relative Dehn functions associated with two finite relative presentations. If
![]() $\Delta _1$
takes only finite values, then
$\Delta _1$
takes only finite values, then
![]() $\Delta _2$
takes only finite values, and
$\Delta _2$
takes only finite values, and
![]() $\Delta _1\asymp \Delta _2$
.
$\Delta _1\asymp \Delta _2$
.
The Dehn function of a pair
![]() $(G,\mathcal{H})$
is well defined if it takes only finite values. This can be characterized in terms of fine graphs as follows.
$(G,\mathcal{H})$
is well defined if it takes only finite values. This can be characterized in terms of fine graphs as follows.
Definition 2.8 (Cayley–Abels graph for pairs). A Cayley–Abels graph of the pair
![]() $(G,\mathcal{H})$
is a connected cocompact simplicial
$(G,\mathcal{H})$
is a connected cocompact simplicial
![]() $G$
-graph
$G$
-graph
![]() $\Gamma$
such that:
$\Gamma$
such that:
-
1. edge
 $G$
-stabilizers are finite,
$G$
-stabilizers are finite,
-
2. vertex
 $G$
-stabilizers are either finite or conjugates of subgroups in
$G$
-stabilizers are either finite or conjugates of subgroups in
 $\mathcal{H}$
,
$\mathcal{H}$
, -
3. every
 $H\in \mathcal{H}$
is the
$H\in \mathcal{H}$
is the
 $G$
-stabilizer of a vertex of
$G$
-stabilizer of a vertex of
 $\Gamma$
, and
$\Gamma$
, and
-
4. any pair of vertices of
 $\Gamma$
with the same
$\Gamma$
with the same
 $G$
-stabilizer
$G$
-stabilizer
 $H\in \mathcal{H}$
are in the same
$H\in \mathcal{H}$
are in the same
 $G$
-orbit if
$G$
-orbit if
 $H$
is infinite.
$H$
is infinite.
Theorem 2.9.
Let
![]() $(G,\mathcal{H})$
be a proper pair. The following statements are equivalent.
$(G,\mathcal{H})$
be a proper pair. The following statements are equivalent.
-
1. The Dehn function
 $\Delta _{G,\mathcal{H}}$
is well defined.
$\Delta _{G,\mathcal{H}}$
is well defined.
-
2.
 $(G,\mathcal{H})$
is finitely presented and there is a fine Cayley–Abels graph of
$(G,\mathcal{H})$
is finitely presented and there is a fine Cayley–Abels graph of
 $(G,\mathcal{H})$
.
$(G,\mathcal{H})$
. -
3.
 $(G,\mathcal{H})$
is finitely presented and every Cayley–Abels graph of
$(G,\mathcal{H})$
is finitely presented and every Cayley–Abels graph of
 $(G,\mathcal{H})$
is fine.
$(G,\mathcal{H})$
is fine.
Theorem 2.9 is essentially [Reference Hughes, Martínez-Pedroza and Saldana12, Theorem E] together with a result on Cayley–Abels graphs from [Reference Arora and Martínez-Pedroza2, Theorem H]. This is described below.
Concrete examples of Cayley–Abels graphs can be exhibited using the following construction introduced by Farb [Reference Farb10]; see also [Reference Hruska13].
Definition 2.10 (Coned-off Cayley graph). Let
![]() $(G,\mathcal{H})$
be a pair, and let
$(G,\mathcal{H})$
be a pair, and let
![]() $S$
be a finite relative generating set of
$S$
be a finite relative generating set of
![]() $G$
with respect to
$G$
with respect to
![]() $\mathcal{H}$
. Denote by
$\mathcal{H}$
. Denote by
![]() $G/\mathcal{H}$
the set of all cosets
$G/\mathcal{H}$
the set of all cosets
![]() $gH$
with
$gH$
with
![]() $g\in G$
and
$g\in G$
and
![]() $P\in \mathcal{H}$
. The coned-off Cayley graph
$P\in \mathcal{H}$
. The coned-off Cayley graph
![]() $\hat \Gamma (G,\mathcal{H},S)$
is the graph with vertex set
$\hat \Gamma (G,\mathcal{H},S)$
is the graph with vertex set
![]() $G\cup G/\mathcal{H}$
and edges of the following type
$G\cup G/\mathcal{H}$
and edges of the following type
-
•
 $\{g,gs\}$
for
$\{g,gs\}$
for
 $s\in S$
and
$s\in S$
and
 $g\in G$
,
$g\in G$
, -
•
 $\{x, gH\}$
for
$\{x, gH\}$
for
 $g\in G$
,
$g\in G$
,
 $H\in \mathcal{H}$
and
$H\in \mathcal{H}$
and
 $x\in gH$
.
$x\in gH$
.
That a pair
![]() $(G,\mathcal{H})$
has a well-defined function is characterized in terms of fineness of coned-off Cayley graphs.
$(G,\mathcal{H})$
has a well-defined function is characterized in terms of fineness of coned-off Cayley graphs.
Theorem 2.11. [Reference Hughes, Martínez-Pedroza and Saldana12, Theorem E] Let
![]() $(G,\mathcal{H})$
be a finitely presented pair with a finite generating set
$(G,\mathcal{H})$
be a finitely presented pair with a finite generating set
![]() $S$
. The Dehn function
$S$
. The Dehn function
![]() $\Delta _{G,\mathcal{H}}$
is well defined if and only if the coned-off Cayley graph
$\Delta _{G,\mathcal{H}}$
is well defined if and only if the coned-off Cayley graph
![]() $\hat \Gamma (G,\mathcal{H},S)$
is fine.
$\hat \Gamma (G,\mathcal{H},S)$
is fine.
Every coned-off Cayley graph
![]() $\hat \Gamma (G,\mathcal{H},S)$
with
$\hat \Gamma (G,\mathcal{H},S)$
with
![]() $S$
a finite relative generating set is a Cayley–Abels graph. The following result implies that coned-off Cayley graphs are, up to quasi-isometry, independent of the choice of finite generating set, and we denote them by
$S$
a finite relative generating set is a Cayley–Abels graph. The following result implies that coned-off Cayley graphs are, up to quasi-isometry, independent of the choice of finite generating set, and we denote them by
![]() $\hat \Gamma (G, \mathcal{H})$
. Observe now that Theorem 2.9 also follows from the following result.
$\hat \Gamma (G, \mathcal{H})$
. Observe now that Theorem 2.9 also follows from the following result.
Theorem 2.12. [Reference Arora and Martínez-Pedroza2, Theorem H] If
![]() $\Gamma$
and
$\Gamma$
and
![]() $\Delta$
are Cayley–Abels graphs of the proper pair
$\Delta$
are Cayley–Abels graphs of the proper pair
![]() $(G,\mathcal{H})$
, then:
$(G,\mathcal{H})$
, then:
-
1.
 $\Gamma$
and
$\Gamma$
and
 $\Delta$
are quasi-isometric, and
$\Delta$
are quasi-isometric, and
-
2.
 $\Gamma$
is fine if and only if
$\Gamma$
is fine if and only if
 $\Delta$
is fine.
$\Delta$
is fine.
3. Combination theorems for graphs
In this section, we state two technical results, Theorems 3.1 and 3.2, which will be proven in the subsequent sections. The section includes how to deduce the main results of the article, Theorems 1.2 and 1.3, from these technical results.
Theorem 3.1.
For
![]() $i\in \{ 1,2\}$
, let
$i\in \{ 1,2\}$
, let
![]() $(G_i, \mathcal{H}_i\cup \{K_i\})$
be a pair and
$(G_i, \mathcal{H}_i\cup \{K_i\})$
be a pair and
![]() $\partial _i\;:\; C\to K_i$
a group monomorphism. Let
$\partial _i\;:\; C\to K_i$
a group monomorphism. Let
![]() $G=G_1\ast _C G_2$
denote the amalgamated product determined by
$G=G_1\ast _C G_2$
denote the amalgamated product determined by
![]() $G_1\xleftarrow{\partial _1}C\xrightarrow{\partial _2}G_2$
, and
$G_1\xleftarrow{\partial _1}C\xrightarrow{\partial _2}G_2$
, and
![]() $\mathcal{H}=\mathcal{H}_1\cup \mathcal{H}_2$
. Let
$\mathcal{H}=\mathcal{H}_1\cup \mathcal{H}_2$
. Let
![]() $\Gamma _i$
be a
$\Gamma _i$
be a
![]() $G_i$
-graph that has a vertex
$G_i$
-graph that has a vertex
![]() $x_i$
with
$x_i$
with
![]() $G_i$
-stabilizer
$G_i$
-stabilizer
![]() $K_i$
. Then there is a
$K_i$
. Then there is a
![]() $G$
-graph
$G$
-graph
![]() $\Gamma$
with the following properties:
$\Gamma$
with the following properties:
-
1.
 $\Gamma$
has a vertex
$\Gamma$
has a vertex
 $z$
such that the
$z$
such that the
 $G$
-stabilizer
$G$
-stabilizer
 $G_z=\langle K_1,K_2\rangle$
, and there is a
$G_z=\langle K_1,K_2\rangle$
, and there is a
 $G_i$
-equivariant inclusion
$G_i$
-equivariant inclusion
 $\Gamma _i\hookrightarrow \Gamma$
that maps
$\Gamma _i\hookrightarrow \Gamma$
that maps
 $x_i$
to
$x_i$
to
 $z$
.
$z$
. -
2. If
 $\Gamma _i$
is connected for
$\Gamma _i$
is connected for
 $i=1,2$
, then
$i=1,2$
, then
 $\Gamma$
is connected.
$\Gamma$
is connected.
-
3. If every
 $H\in \mathcal{H}_i\cup \{K_i\}$
is the
$H\in \mathcal{H}_i\cup \{K_i\}$
is the
 $G_i$
-stabilizer of a vertex of
$G_i$
-stabilizer of a vertex of
 $\Gamma _i$
for
$\Gamma _i$
for
 $i=1,2$
, then every
$i=1,2$
, then every
 $H\in \mathcal{H}\cup \{\langle K_1,K_2 \rangle \}$
is the
$H\in \mathcal{H}\cup \{\langle K_1,K_2 \rangle \}$
is the
 $G$
-stabilizer of a vertex of
$G$
-stabilizer of a vertex of
 $\Gamma$
.
$\Gamma$
. -
4. If vertex
 $G_i$
-stabilizers in
$G_i$
-stabilizers in
 $\Gamma _i$
are finite or conjugates of subgroups in
$\Gamma _i$
are finite or conjugates of subgroups in
 $\mathcal{H}_i\cup \{ K_i\}$
for
$\mathcal{H}_i\cup \{ K_i\}$
for
 $i=1,2$
, then vertex
$i=1,2$
, then vertex
 $G$
-stabilizers in
$G$
-stabilizers in
 $\Gamma$
are finite or conjugates of subgroups in
$\Gamma$
are finite or conjugates of subgroups in
 $\mathcal{H}\cup \{ \langle K_1,K_2\rangle \}$
.
$\mathcal{H}\cup \{ \langle K_1,K_2\rangle \}$
. -
5. If
 $\Gamma _i$
has finite edge
$\Gamma _i$
has finite edge
 $G_i$
-stabilizers for
$G_i$
-stabilizers for
 $i=1,2$
, then
$i=1,2$
, then
 $\Gamma$
has finite edge
$\Gamma$
has finite edge
 $G$
-stabilizers.
$G$
-stabilizers.
-
6. If
 $\Gamma _i$
has finitely many
$\Gamma _i$
has finitely many
 $G_i$
-orbits of vertices (edges) for
$G_i$
-orbits of vertices (edges) for
 $i=1,2$
, then
$i=1,2$
, then
 $\Gamma$
has finitely many
$\Gamma$
has finitely many
 $G$
-orbits of vertices (resp. edges).
$G$
-orbits of vertices (resp. edges).
-
7. If
 $\Gamma _i$
is fine for
$\Gamma _i$
is fine for
 $i=1,2$
, then
$i=1,2$
, then
 $\Gamma$
is fine.
$\Gamma$
is fine.
-
8. If
 $\Gamma _i$
is fine at
$\Gamma _i$
is fine at
 $V_\infty (\Gamma _i)$
for
$V_\infty (\Gamma _i)$
for
 $i=1,2$
, then
$i=1,2$
, then
 $\Gamma$
is fine at
$\Gamma$
is fine at
 $V_\infty (\Gamma )$
.
$V_\infty (\Gamma )$
. -
9. If
 $\Gamma _i$
is hyperbolic for
$\Gamma _i$
is hyperbolic for
 $i=1,2$
, then
$i=1,2$
, then
 $\Gamma$
is hyperbolic.
$\Gamma$
is hyperbolic.
-
10. If
 $\Gamma _i$
is simplicial for
$\Gamma _i$
is simplicial for
 $i=1,2$
, then
$i=1,2$
, then
 $\Gamma$
is simplicial.
$\Gamma$
is simplicial.
Let us explain how Theorem 1.2 follows from the above result.
Proof of Theorem 1.2. For the first statement, suppose
![]() $\mathcal{H}_i\cup \{K_i\}$
is hyperbolically embedded in
$\mathcal{H}_i\cup \{K_i\}$
is hyperbolically embedded in
![]() $G_i$
. Then
$G_i$
. Then
![]() $\mathcal{H}_i\cup \{K_i\}$
is an almost malnormal collection of subgroups of
$\mathcal{H}_i\cup \{K_i\}$
is an almost malnormal collection of subgroups of
![]() $G_i$
by [Reference Dahmani, Guirardel and Osin9, Prop. 4.33]. In particular,
$G_i$
by [Reference Dahmani, Guirardel and Osin9, Prop. 4.33]. In particular,
![]() $(G_i, \mathcal{H}_i\cup \{K_i\})$
is a proper pair. By Theorem 2.2, there is a
$(G_i, \mathcal{H}_i\cup \{K_i\})$
is a proper pair. By Theorem 2.2, there is a
![]() $(G_i, \mathcal{H}_i\cup \{K_i\})$
-graph
$(G_i, \mathcal{H}_i\cup \{K_i\})$
-graph
![]() $\Gamma _i$
. Let
$\Gamma _i$
. Let
![]() $x_i$
be a vertex of
$x_i$
be a vertex of
![]() $\Gamma _i$
with
$\Gamma _i$
with
![]() $G_i$
-stabilizer
$G_i$
-stabilizer
![]() $K_i$
. Applying Theorem 3.1 to
$K_i$
. Applying Theorem 3.1 to
![]() $\Gamma _1$
,
$\Gamma _1$
,
![]() $\Gamma _2$
,
$\Gamma _2$
,
![]() $x_1$
and
$x_1$
and
![]() $x_2$
, we obtain a
$x_2$
, we obtain a
![]() $(G_1\ast _CG_2, \mathcal{H}\cup \{\langle K_1,K_2 \rangle \})$
-graph. Note that
$(G_1\ast _CG_2, \mathcal{H}\cup \{\langle K_1,K_2 \rangle \})$
-graph. Note that
![]() $(G_1\ast _CG_2, \mathcal{H}\cup \{\langle K_1,K_2 \rangle \})$
is a proper pair by a standard argument using normal forms. Then invoke Theorem 2.2 to obtain that
$(G_1\ast _CG_2, \mathcal{H}\cup \{\langle K_1,K_2 \rangle \})$
is a proper pair by a standard argument using normal forms. Then invoke Theorem 2.2 to obtain that
![]() $\mathcal{H}\cup \{\langle K_1,K_2 \rangle \}$
is hyperbolically embedded in
$\mathcal{H}\cup \{\langle K_1,K_2 \rangle \}$
is hyperbolically embedded in
![]() $G_1\ast _CG_2$
.
$G_1\ast _CG_2$
.
The second statement is proved analogously. Suppose the relative Dehn function of
![]() $(G_i,\mathcal{H}_i\cup \{K_i\})$
is well defined. By [Reference Osin17, Prop. 2.36], the pair
$(G_i,\mathcal{H}_i\cup \{K_i\})$
is well defined. By [Reference Osin17, Prop. 2.36], the pair
![]() $(G_i,\mathcal{H}_i\cup \{K_i\})$
is proper. It follows that
$(G_i,\mathcal{H}_i\cup \{K_i\})$
is proper. It follows that
![]() $(G_1\ast _CG_2, \mathcal{H}\cup \{\langle K_1,K_2 \rangle \})$
is also a proper pair by a standard argument using normal forms. By Theorem 2.9,
$(G_1\ast _CG_2, \mathcal{H}\cup \{\langle K_1,K_2 \rangle \})$
is also a proper pair by a standard argument using normal forms. By Theorem 2.9,
![]() $(G_i,\mathcal{H}_i\cup \{K_i\})$
is finitely presented and admits a fine Cayley–Abels graph
$(G_i,\mathcal{H}_i\cup \{K_i\})$
is finitely presented and admits a fine Cayley–Abels graph
![]() $\Gamma _i$
. In particular, there is a vertex
$\Gamma _i$
. In particular, there is a vertex
![]() $x_i\in \Gamma _i$
with
$x_i\in \Gamma _i$
with
![]() $G_i$
-stabilizer equal to
$G_i$
-stabilizer equal to
![]() $K_i$
. Apply Theorem 3.1 to
$K_i$
. Apply Theorem 3.1 to
![]() $\Gamma _1$
,
$\Gamma _1$
,
![]() $\Gamma _2$
and the vertices
$\Gamma _2$
and the vertices
![]() $x_1,x_2$
to obtain a fine Cayley–Abels graph
$x_1,x_2$
to obtain a fine Cayley–Abels graph
![]() $\Gamma$
for the pair
$\Gamma$
for the pair
![]() $(G_1\ast _CG_2, \mathcal{H}\cup \{\langle K_1,K_2 \rangle \})$
. Since
$(G_1\ast _CG_2, \mathcal{H}\cup \{\langle K_1,K_2 \rangle \})$
. Since
![]() $(G_1\ast _CG_2, \mathcal{H}\cup \{\langle K_1,K_2 \rangle \})$
is finitely presented by Lemma 2.5, then Theorem 2.9 implies that the relative Dehn function of
$(G_1\ast _CG_2, \mathcal{H}\cup \{\langle K_1,K_2 \rangle \})$
is finitely presented by Lemma 2.5, then Theorem 2.9 implies that the relative Dehn function of
![]() $(G_1\ast _CG_2, \mathcal{H}\cup \{\langle K_1,K_2 \rangle \})$
is well defined.
$(G_1\ast _CG_2, \mathcal{H}\cup \{\langle K_1,K_2 \rangle \})$
is well defined.
Theorem 3.2.
Let
![]() $(G, \mathcal{H} \cup \{K,L\})$
be a pair with
$(G, \mathcal{H} \cup \{K,L\})$
be a pair with
![]() $K\neq L$
,
$K\neq L$
,
![]() $C\leq K$
, and
$C\leq K$
, and
![]() $\varphi \;:\; C\to L$
a group monomorphism. Let
$\varphi \;:\; C\to L$
a group monomorphism. Let
![]() $G\ast _\varphi$
denote the HNN-extension
$G\ast _\varphi$
denote the HNN-extension
![]() $\langle G, t\mid t c t^{-1} =\varphi (c) \text{ for all $c\in C$} \rangle$
. Let
$\langle G, t\mid t c t^{-1} =\varphi (c) \text{ for all $c\in C$} \rangle$
. Let
![]() $\Delta$
be a
$\Delta$
be a
![]() $G$
-graph that has vertices
$G$
-graph that has vertices
![]() $x$
and
$x$
and
![]() $y$
such that their
$y$
such that their
![]() $G$
-stabilizers are
$G$
-stabilizers are
![]() $K$
and
$K$
and
![]() $L$
, respectively, and their
$L$
, respectively, and their
![]() $G$
-orbits are disjoint. Then there is a
$G$
-orbits are disjoint. Then there is a
![]() $G\ast _\varphi$
-graph
$G\ast _\varphi$
-graph
![]() $\Gamma$
with the following properties:
$\Gamma$
with the following properties:
-
1.
 $\Gamma$
has a vertex
$\Gamma$
has a vertex
 $z$
such that
$z$
such that
 $G_z=\langle K^t,L\rangle$
, and there is a
$G_z=\langle K^t,L\rangle$
, and there is a
 $G$
-equivariant inclusion
$G$
-equivariant inclusion
 $\Delta \hookrightarrow \Gamma$
such that
$\Delta \hookrightarrow \Gamma$
such that
 $x\mapsto t^{-1}.z$
and
$x\mapsto t^{-1}.z$
and
 $y\mapsto z$
.
$y\mapsto z$
. -
2. If
 $\Delta$
is connected, then
$\Delta$
is connected, then
 $\Gamma$
is connected.
$\Gamma$
is connected.
-
3. If every
 $H\in \mathcal{H}\cup \{K,L\}$
is the
$H\in \mathcal{H}\cup \{K,L\}$
is the
 $G$
-stabilizer of a vertex of
$G$
-stabilizer of a vertex of
 $\Delta$
, then every
$\Delta$
, then every
 $H\in \mathcal{H}\cup \{\langle K^t,L \rangle \}$
is the
$H\in \mathcal{H}\cup \{\langle K^t,L \rangle \}$
is the
 $G\ast _\varphi$
-stabilizer of a vertex of
$G\ast _\varphi$
-stabilizer of a vertex of
 $\Gamma$
.
$\Gamma$
. -
4. If vertex
 $G$
-stabilizers in
$G$
-stabilizers in
 $\Delta$
are finite or conjugates of subgroups in
$\Delta$
are finite or conjugates of subgroups in
 $\mathcal{H}\cup \{ K,L\}$
, then vertex
$\mathcal{H}\cup \{ K,L\}$
, then vertex
 $G\ast _\varphi$
-stabilizers in
$G\ast _\varphi$
-stabilizers in
 $\Gamma$
are finite or conjugates of subgroups in
$\Gamma$
are finite or conjugates of subgroups in
 $\mathcal{H}\cup \{ \langle K^t,L\rangle \}$
.
$\mathcal{H}\cup \{ \langle K^t,L\rangle \}$
. -
5. If
 $\Delta$
has finite edge
$\Delta$
has finite edge
 $G$
-stabilizers, then
$G$
-stabilizers, then
 $\Gamma$
has finite edge
$\Gamma$
has finite edge
 $G\ast _\varphi$
-stabilizers.
$G\ast _\varphi$
-stabilizers.
-
6. If
 $\Delta$
has finitely many
$\Delta$
has finitely many
 $G$
-orbits of vertices (edges), then
$G$
-orbits of vertices (edges), then
 $\Gamma$
has finitely many
$\Gamma$
has finitely many
 $G\ast _\varphi$
-orbits of vertices (resp. edges).
$G\ast _\varphi$
-orbits of vertices (resp. edges).
-
7. If
 $\Delta$
is fine, then
$\Delta$
is fine, then
 $\Gamma$
is fine.
$\Gamma$
is fine.
-
8. If
 $\Delta$
is fine at
$\Delta$
is fine at
 $V_\infty (\Delta )$
, then
$V_\infty (\Delta )$
, then
 $\Gamma$
is fine at
$\Gamma$
is fine at
 $V_\infty (\Gamma )$
.
$V_\infty (\Gamma )$
. -
9. If
 $\Delta$
is hyperbolic, then
$\Delta$
is hyperbolic, then
 $\Gamma$
is hyperbolic.
$\Gamma$
is hyperbolic.
Proof of Theorem 1.3. This proof is completely analogous to the proof of Theorem 1.2: invoke Theorem 3.2 and Lemma 2.6 instead of Theorem 3.1 and Lemma 2.5, respectively.
4. Amalgamated products and graphs
This section describes an argument proving Theorem 3.1. While the statement of this result seems intuitive, we are not aware of a full account of those techniques in a common framework, so this section provides a detailed construction.
4.1. Pushouts in the category of
 $G$
-sets
$G$
-sets
Let
![]() $\phi \;:\; R\to S$
and
$\phi \;:\; R\to S$
and
![]() $\psi \;:\; R \to T$
be
$\psi \;:\; R \to T$
be
![]() $G$
-maps. The pushout of
$G$
-maps. The pushout of
![]() $\phi$
and
$\phi$
and
![]() $\psi$
is defined as follows. Let
$\psi$
is defined as follows. Let
![]() $Z$
be the
$Z$
be the
![]() $G$
-set obtained as the quotient of the disjoint union of
$G$
-set obtained as the quotient of the disjoint union of
![]() $G$
-sets
$G$
-sets
![]() $S\sqcup T$
by the equivalence relation generated by all pairs
$S\sqcup T$
by the equivalence relation generated by all pairs
![]() $s\sim t$
with
$s\sim t$
with
![]() $s\in S$
and
$s\in S$
and
![]() $t\in T$
satisfying that there is
$t\in T$
satisfying that there is
![]() $r\in R$
such that
$r\in R$
such that
![]() $\phi (r)=s$
and
$\phi (r)=s$
and
![]() $\psi (r)=t$
. There are canonical
$\psi (r)=t$
. There are canonical
![]() $G$
-maps
$G$
-maps
![]() $\imath \;:\; S \to Z$
and
$\imath \;:\; S \to Z$
and
![]() $\jmath \;:\; T \to Z$
such that
$\jmath \;:\; T \to Z$
such that
![]() $\imath \circ \phi = \jmath \circ \psi$
. This construction satisfies the universal property of pushouts in the category of
$\imath \circ \phi = \jmath \circ \psi$
. This construction satisfies the universal property of pushouts in the category of
![]() $G$
-sets.
$G$
-sets.
Proposition 4.1.
Let
![]() $\phi \;:\; R\to S$
and
$\phi \;:\; R\to S$
and
![]() $\psi \;:\; R \to T$
be
$\psi \;:\; R \to T$
be
![]() $G$
-maps. Consider the pushout
$G$
-maps. Consider the pushout

of
![]() $\phi$
and
$\phi$
and
![]() $\psi$
. Suppose there is
$\psi$
. Suppose there is
![]() $r\in R$
such that
$r\in R$
such that
![]() $R=G.r$
. If
$R=G.r$
. If
![]() $s=\phi (r)$
,
$s=\phi (r)$
,
![]() $t=\psi (r)$
and
$t=\psi (r)$
and
![]() $z=\imath (s)$
, then the
$z=\imath (s)$
, then the
![]() $G$
-stabilizer
$G$
-stabilizer
![]() $G_z$
equals the subgroup
$G_z$
equals the subgroup
![]() $\langle G_s,G_t \rangle$
.
$\langle G_s,G_t \rangle$
.
Proof. Since
![]() $\imath$
and
$\imath$
and
![]() $\jmath$
are
$\jmath$
are
![]() $G$
-maps,
$G$
-maps,
![]() $\langle G_s,G_t \rangle \leq G_z$
. Conversely, let
$\langle G_s,G_t \rangle \leq G_z$
. Conversely, let
![]() $g\in G_z$
. If
$g\in G_z$
. If
![]() $g\in G_s$
then
$g\in G_s$
then
![]() $g\in \langle G_s, G_t\rangle$
. Suppose
$g\in \langle G_s, G_t\rangle$
. Suppose
![]() $g\not \in G_s$
.
$g\not \in G_s$
.
Let
![]() $r_0$
denote the element
$r_0$
denote the element
![]() $r\in R$
in the statement, in particular,
$r\in R$
in the statement, in particular,
![]() $s=\phi (r_0)$
,
$s=\phi (r_0)$
,
![]() $t=\psi (r_0)$
and
$t=\psi (r_0)$
and
![]() $R=G.r_0$
. Since
$R=G.r_0$
. Since
![]() $\jmath (t)=\imath (g.s)$
, the definition of
$\jmath (t)=\imath (g.s)$
, the definition of
![]() $Z$
as a collection of equivalence classes in
$Z$
as a collection of equivalence classes in
![]() $S\sqcup T$
implies that there is a sequence
$S\sqcup T$
implies that there is a sequence
![]() $r'_{\!\!0},r_1,r'_{\!\!1}\ldots, r_k, r'_{\!\!k}$
of elements of
$r'_{\!\!0},r_1,r'_{\!\!1}\ldots, r_k, r'_{\!\!k}$
of elements of
![]() $R$
such that
$R$
such that
Let
![]() $s_i=\phi (r'_{\!\!i-1})=\phi (r_i)$
and
$s_i=\phi (r'_{\!\!i-1})=\phi (r_i)$
and
![]() $t_i=\psi (r_i)=\psi (r'_{\!\!i})$
. Since
$t_i=\psi (r_i)=\psi (r'_{\!\!i})$
. Since
![]() $R=G.r_0$
, there are elements
$R=G.r_0$
, there are elements
![]() $a_0,a_1,\ldots,a_k$
and
$a_0,a_1,\ldots,a_k$
and
![]() $b_0,b_1,\ldots, b_{k-1}$
of
$b_0,b_1,\ldots, b_{k-1}$
of
![]() $G$
such that
$G$
such that
for
![]() $0\leq i\leq k$
and
$0\leq i\leq k$
and
![]() $0\leq j\lt k$
. Then
$0\leq j\lt k$
. Then
and hence
![]() $ a_k b_{k-1} a_{k-1} \ldots b_0a_0 \in gG_s.$
Since
$ a_k b_{k-1} a_{k-1} \ldots b_0a_0 \in gG_s.$
Since
![]() $G_s \leq \langle G_s, G_t \rangle$
, to prove that
$G_s \leq \langle G_s, G_t \rangle$
, to prove that
![]() $g\in \langle G_s, G_t \rangle$
is enough to show that
$g\in \langle G_s, G_t \rangle$
is enough to show that
![]() $a_i, b_j \in \langle G_s, G_t \rangle$
. We will argue by induction.
$a_i, b_j \in \langle G_s, G_t \rangle$
. We will argue by induction.
First note that since
![]() $\phi$
and
$\phi$
and
![]() $\psi$
are
$\psi$
are
![]() $G$
-maps
$G$
-maps
and hence
Moreover,
![]() $t_i=\psi (r_i)=\psi (r'_{\!\!i})=\psi (a_i.r_i)=a_i.t_i$
implies
$t_i=\psi (r_i)=\psi (r'_{\!\!i})=\psi (a_i.r_i)=a_i.t_i$
implies
and analogously
![]() $s_{j+1}=\phi (r_{j+1})=\phi (b_j.r'_{\!\!j})=b_j.s_{j+1}$
implies
$s_{j+1}=\phi (r_{j+1})=\phi (b_j.r'_{\!\!j})=b_j.s_{j+1}$
implies
Since
![]() $t_0=t$
and
$t_0=t$
and
![]() $s_0=s$
, we have that
$s_0=s$
, we have that
Suppose
![]() $i\lt k$
,
$i\lt k$
,
![]() $a_i,b_i\in \langle G_s, G_t \rangle$
,
$a_i,b_i\in \langle G_s, G_t \rangle$
,
![]() $G_{s_i}\leq \langle G_s, G_t \rangle$
and
$G_{s_i}\leq \langle G_s, G_t \rangle$
and
![]() $G_{t_i}\leq \langle G_s, G_t \rangle$
. Then
$G_{t_i}\leq \langle G_s, G_t \rangle$
. Then
and hence
In the case that
![]() $i+1\lt k$
,
$i+1\lt k$
,
Therefore, by induction,
![]() $a_i,b_j\in \langle G_s, G_t \rangle$
for
$a_i,b_j\in \langle G_s, G_t \rangle$
for
![]() $0\leq i\leq k$
and
$0\leq i\leq k$
and
![]() $0\leq j\lt k$
.
$0\leq j\lt k$
.
4.2. Extending actions on sets
In the case that
![]() $K$
is a subgroup of
$K$
is a subgroup of
![]() $G$
and
$G$
and
![]() $S$
is a
$S$
is a
![]() $K$
-set, one can extend the
$K$
-set, one can extend the
![]() $K$
-action on
$K$
-action on
![]() $S$
to a
$S$
to a
![]() $G$
-set
$G$
-set
![]() $G\times _K S$
that we now describe. Up to isomorphism of
$G\times _K S$
that we now describe. Up to isomorphism of
![]() $K$
-sets, we can assume that
$K$
-sets, we can assume that
![]() $S$
is a disjoint union of
$S$
is a disjoint union of
![]() $K$
-sets:
$K$
-sets:
where
![]() $K/K_i$
is the
$K/K_i$
is the
![]() $K$
-set consisting of left cosets of a subgroup
$K$
-set consisting of left cosets of a subgroup
![]() $K_i$
of
$K_i$
of
![]() $K$
. Then the
$K$
. Then the
![]() $G$
-set
$G$
-set
![]() $G\times _K S$
is defined as a disjoint union of
$G\times _K S$
is defined as a disjoint union of
![]() $G$
-sets:
$G$
-sets:
Observe that the canonical
![]() $K$
-map
$K$
-map
is injective. This construction satisfies a number of useful properties that we summarize in the following proposition.
For
![]() $n$
a natural number and a set
$n$
a natural number and a set
![]() $X$
, let
$X$
, let
![]() $[X]^n$
denote the collection of subsets of
$[X]^n$
denote the collection of subsets of
![]() $X$
of cardinality
$X$
of cardinality
![]() $n$
. If
$n$
. If
![]() $X$
is a
$X$
is a
![]() $G$
-set, then
$G$
-set, then
![]() $[X]^n$
is a
$[X]^n$
is a
![]() $G$
-set with action defined as
$G$
-set with action defined as
![]() $g.\{x_1,\ldots,x_n\}=\{g.x_1,\ldots,g.x_n\}$
.
$g.\{x_1,\ldots,x_n\}=\{g.x_1,\ldots,g.x_n\}$
.
Proposition 4.2.
Let
![]() $K\leq G$
and
$K\leq G$
and
![]() $S$
a
$S$
a
![]() $K$
-set.
$K$
-set.
-
1. The canonical
 $K$
-map
$K$
-map
 $ \imath \;:\; S \to G\times _K S$
induces a bijection of orbit spaces
$ \imath \;:\; S \to G\times _K S$
induces a bijection of orbit spaces
 $S/K \to (G\times _K S)/G$
.
$S/K \to (G\times _K S)/G$
. -
2. For each
 $s\in S$
, the
$s\in S$
, the
 $K$
-stabilizer
$K$
-stabilizer
 $K_s$
equals the
$K_s$
equals the
 $G$
-stabilizer
$G$
-stabilizer
 $G_{\imath (s)}$
.
$G_{\imath (s)}$
. -
3. If
 $T$
is a
$T$
is a
 $G$
-set and
$G$
-set and
 $f\;:\; S \to T$
is
$f\;:\; S \to T$
is
 $K$
-equivariant, then there is a unique
$K$
-equivariant, then there is a unique
 $G$
-map
$G$
-map
 $\tilde f\;:\; G\times _K S \to T$
such that
$\tilde f\;:\; G\times _K S \to T$
such that
 $\tilde f \circ \imath = f$
.
$\tilde f \circ \imath = f$
. -
4. If
 $\imath (S)\cap g.\imath (S)\neq \emptyset$
for
$\imath (S)\cap g.\imath (S)\neq \emptyset$
for
 $g\in G$
, then
$g\in G$
, then
 $g\in K$
and
$g\in K$
and
 $\imath (S)=g.\imath (S)$
.
$\imath (S)=g.\imath (S)$
. -
5. In part three, if
 $f$
induces an injective map
$f$
induces an injective map
 $S/K \to T/G$
and
$S/K \to T/G$
and
 $K_s = G_{f(s)}$
for every
$K_s = G_{f(s)}$
for every
 $s\in S$
, then
$s\in S$
, then
 $\tilde f$
is injective.
$\tilde f$
is injective.
-
6. Let
 $\jmath \;:\; [S]^n \to G\times _K[S]^n$
be the canonical map. Then for every
$\jmath \;:\; [S]^n \to G\times _K[S]^n$
be the canonical map. Then for every
 $n\in \mathbb N$
, there is a
$n\in \mathbb N$
, there is a
 $G$
-equivariant injection
$G$
-equivariant injection
 $\hat \imath \;:\; G\times _K [S]^n \to [G\times _K S]^n$
such that
$\hat \imath \;:\; G\times _K [S]^n \to [G\times _K S]^n$
such that
 $\hat \imath \circ \jmath = \bar \imath$
where
$\hat \imath \circ \jmath = \bar \imath$
where
 $\bar \imath \;:\; [S]^n \to [G\times _K S]^n$
is the natural
$\bar \imath \;:\; [S]^n \to [G\times _K S]^n$
is the natural
 $K$
-map induced by
$K$
-map induced by
 $\imath \;:\; S \to G\times _K S$
.
$\imath \;:\; S \to G\times _K S$
.
Proof. The first four statements are observations. For the fifth statement, suppose
![]() $\tilde f(\imath (s_1) ) = \tilde f(g.\imath (s_2))$
. Then
$\tilde f(\imath (s_1) ) = \tilde f(g.\imath (s_2))$
. Then
![]() $f( s_1 )=g.f( s_2 )$
. Since the map
$f( s_1 )=g.f( s_2 )$
. Since the map
![]() $S/K\to T/G$
induced by
$S/K\to T/G$
induced by
![]() $f$
is injective, we have that
$f$
is injective, we have that
![]() $s_1$
and
$s_1$
and
![]() $s_2$
are in the same
$s_2$
are in the same
![]() $K$
-orbit in
$K$
-orbit in
![]() $S$
, say
$S$
, say
![]() $s_2=k.s_1$
for
$s_2=k.s_1$
for
![]() $k\in K$
. It follows that
$k\in K$
. It follows that
![]() $f( s_1 )=gk.f( s_1 )$
, and since
$f( s_1 )=gk.f( s_1 )$
, and since
![]() $K_{s_1} = G_{f(s_1)}$
, we have that
$K_{s_1} = G_{f(s_1)}$
, we have that
![]() $gk\in K_{s_1}$
. Therefore
$gk\in K_{s_1}$
. Therefore
![]() $\imath (s_1) =\imath (gk.s_1)= g.\imath (ks_1) =g.\imath (s_2)$
.
$\imath (s_1) =\imath (gk.s_1)= g.\imath (ks_1) =g.\imath (s_2)$
.
The sixth statement is proved as follows. The
![]() $K$
-map
$K$
-map
![]() $\imath \;:\; S \to G\times _K S$
naturally induces a
$\imath \;:\; S \to G\times _K S$
naturally induces a
![]() $K$
-map
$K$
-map
![]() $\bar \imath \;:\; [S]^n \to [G\times _K S]^n$
. By the third statement, there is a unique
$\bar \imath \;:\; [S]^n \to [G\times _K S]^n$
. By the third statement, there is a unique
![]() $G$
-map
$G$
-map
![]() $\hat \imath \;:\; G\times _K [S]^n \to [G\times _K S]^n$
such that
$\hat \imath \;:\; G\times _K [S]^n \to [G\times _K S]^n$
such that
![]() $\hat \imath \circ \jmath = \bar \imath$
where
$\hat \imath \circ \jmath = \bar \imath$
where
![]() $\jmath \;:\; [S]^n \to G\times _K[S]^n$
. As a consequence of the fourth statement,
$\jmath \;:\; [S]^n \to G\times _K[S]^n$
. As a consequence of the fourth statement,
![]() $\imath \;:\; [S]^n \to [G\times _K S]^n$
induces an injective map
$\imath \;:\; [S]^n \to [G\times _K S]^n$
induces an injective map
![]() $[S]^n/K \to [G\times _K S]^n/G$
and
$[S]^n/K \to [G\times _K S]^n/G$
and
![]() $K_A = G_{\imath (A)}$
for every
$K_A = G_{\imath (A)}$
for every
![]() $A\in [S]^n$
; therefore,
$A\in [S]^n$
; therefore,
![]() $\hat \imath$
is injective.
$\hat \imath$
is injective.
As the reader might have noticed, this construction is an instance of general categorical phenomena; that formulation will have no use in this article so we will not discuss it.
4.3. Graphs as 1-dimensional complexes
While the objectives of this section only require us to consider simplicial graphs, the category of simplicial graphs does not have pushouts [Reference Stallings20]. For this reason, it is convenient to work within the framework of one-dimensional complexes or equivalently graphs in the sense that we describe below. We will only consider a particular class of pushouts of graphs that behaves well over simplicial graphs. A graph is a triple
![]() $(V,E,r)$
, where
$(V,E,r)$
, where
![]() $V$
and
$V$
and
![]() $E$
are sets, and
$E$
are sets, and
![]() $r\;:\; E \to [V]^2$
is a function where
$r\;:\; E \to [V]^2$
is a function where
![]() $[V]^n$
is the collection of nonempty subsets of
$[V]^n$
is the collection of nonempty subsets of
![]() $V$
of cardinality at most
$V$
of cardinality at most
![]() $n$
. Elements of the set
$n$
. Elements of the set
![]() $V$
and
$V$
and
![]() $E$
are called vertices and edges, respectively; the function
$E$
are called vertices and edges, respectively; the function
![]() $r$
is called the attaching map. For a graph
$r$
is called the attaching map. For a graph
![]() $\Gamma$
, we denote
$\Gamma$
, we denote
![]() $V(\Gamma )$
and
$V(\Gamma )$
and
![]() $E(\Gamma )$
its vertex and edge set, respectively. If
$E(\Gamma )$
its vertex and edge set, respectively. If
![]() $v\in V(\Gamma )$
,
$v\in V(\Gamma )$
,
![]() $e\in E(\Gamma )$
and
$e\in E(\Gamma )$
and
![]() $v\in r(e)$
, then
$v\in r(e)$
, then
![]() $v$
is incident to
$v$
is incident to
![]() $e$
, and
$e$
, and
![]() $v$
is called an endpoint of
$v$
is called an endpoint of
![]() $e$
. Vertices incident to the same edge are called adjacent.
$e$
. Vertices incident to the same edge are called adjacent.
The graph
![]() $(V,E,r)$
is simplicial if every edge has two distinct endpoints and
$(V,E,r)$
is simplicial if every edge has two distinct endpoints and
![]() $r$
is injective. Equivalently,
$r$
is injective. Equivalently,
![]() $(V,E,r)$
is simplicial if
$(V,E,r)$
is simplicial if
![]() $r\;:\; E \to [V]^2$
is injective and its image does not intersect
$r\;:\; E \to [V]^2$
is injective and its image does not intersect
![]() $[V]^1$
.
$[V]^1$
.
A graph
![]() $\Delta$
is a subgraph of a graph
$\Delta$
is a subgraph of a graph
![]() $\Gamma$
if
$\Gamma$
if
![]() $V(\Delta ) \subset V(\Gamma )$
,
$V(\Delta ) \subset V(\Gamma )$
,
![]() $E(\Delta ) \subset E(\Gamma )$
and
$E(\Delta ) \subset E(\Gamma )$
and
![]() $r_\Delta$
equals the restriction of
$r_\Delta$
equals the restriction of
![]() $r_\Gamma$
to
$r_\Gamma$
to
![]() $E(\Delta )$
. Abusing notation, we consider any vertex of a graph
$E(\Delta )$
. Abusing notation, we consider any vertex of a graph
![]() $\Gamma$
as an edgeless subgraph with a single vertex, and any edge
$\Gamma$
as an edgeless subgraph with a single vertex, and any edge
![]() $e$
of
$e$
of
![]() $\Gamma$
as the subgraph with vertex set the set of vertices incident to
$\Gamma$
as the subgraph with vertex set the set of vertices incident to
![]() $e$
in
$e$
in
![]() $\Gamma$
and edge set consisting of only
$\Gamma$
and edge set consisting of only
![]() $e$
.
$e$
.
For a vertex
![]() $u$
of a simplicial graph
$u$
of a simplicial graph
![]() $\Gamma =(V,E,r)$
, let
$\Gamma =(V,E,r)$
, let
![]() $\mathsf{star_\Gamma (u)}$
denote the subgraph with vertex set
$\mathsf{star_\Gamma (u)}$
denote the subgraph with vertex set
![]() $V(\mathsf{star}(u))=\{u\}\cup \{v\in V\mid \text{$v$ is adjacent to $u$}\}$
and edge set
$V(\mathsf{star}(u))=\{u\}\cup \{v\in V\mid \text{$v$ is adjacent to $u$}\}$
and edge set
![]() $E(\mathsf{star}(u)) = \{e\in E\mid \text{the endpoints of $e$ belong to $V(\mathsf{star}(u))$}\}$
and the attaching map is the corresponding restriction of
$E(\mathsf{star}(u)) = \{e\in E\mid \text{the endpoints of $e$ belong to $V(\mathsf{star}(u))$}\}$
and the attaching map is the corresponding restriction of
![]() $r$
.
$r$
.
Our notion of morphism allows the collapse of edges to single vertices. Specifically, a morphism of
![]() $\phi \;:\; (V,E,r) \to (V',E',r')$
of graphs is a pair of maps
$\phi \;:\; (V,E,r) \to (V',E',r')$
of graphs is a pair of maps
![]() $\phi _0\;:\; V\to V'$
and
$\phi _0\;:\; V\to V'$
and
![]() $\phi _1\;:\; E \to V'\cup E'$
such that there is a commutative diagram
$\phi _1\;:\; E \to V'\cup E'$
such that there is a commutative diagram

where the horizontal bottom arrow
![]() $\phi _0$
is the natural
$\phi _0$
is the natural
![]() $G$
-map induced by
$G$
-map induced by
![]() $\phi _0\;:\; V\to V'$
, and
$\phi _0\;:\; V\to V'$
, and
![]() $V'\to [V']^1$
is the natural bijection given by
$V'\to [V']^1$
is the natural bijection given by
![]() $v\mapsto \{v\}$
. Observe that in general for a morphism
$v\mapsto \{v\}$
. Observe that in general for a morphism
![]() $\phi =(\phi _0,\phi _1) \;:\; \Gamma \to \Delta$
of graphs, the map
$\phi =(\phi _0,\phi _1) \;:\; \Gamma \to \Delta$
of graphs, the map
![]() $\phi _0$
does not determine
$\phi _0$
does not determine
![]() $\phi _1$
; however if
$\phi _1$
; however if
![]() $\Delta$
is simplicial then
$\Delta$
is simplicial then
![]() $\phi _0$
determines
$\phi _0$
determines
![]() $\phi _1$
. A morphism
$\phi _1$
. A morphism
![]() $(\phi _0,\phi _1)$
is a monomorphism (also called an embedding) if both maps are injective.
$(\phi _0,\phi _1)$
is a monomorphism (also called an embedding) if both maps are injective.
Given a graph morphism
![]() $\phi =(\phi _0, \phi _1)\;:\; \Gamma \to \Delta$
and a subgraph
$\phi =(\phi _0, \phi _1)\;:\; \Gamma \to \Delta$
and a subgraph
![]() $\Theta$
of
$\Theta$
of
![]() $\Delta$
, the preimage
$\Delta$
, the preimage
![]() $\phi ^{-1}(\Theta )$
is the subgraph of
$\phi ^{-1}(\Theta )$
is the subgraph of
![]() $\Gamma$
with vertex set
$\Gamma$
with vertex set
![]() $\phi _0^{-1}(V(\Theta ))$
and edge set
$\phi _0^{-1}(V(\Theta ))$
and edge set
![]() $\phi _1^{-1}(V(\Theta )\cup E(\Theta ))$
.
$\phi _1^{-1}(V(\Theta )\cup E(\Theta ))$
.
Let
![]() $G$
be a group. A
$G$
be a group. A
![]() $G$
-graph is a graph
$G$
-graph is a graph
![]() $(V,E,r)$
where
$(V,E,r)$
where
![]() $V$
and
$V$
and
![]() $E$
are
$E$
are
![]() $G$
-sets, and
$G$
-sets, and
![]() $r$
is a
$r$
is a
![]() $G$
-map with respect to the natural
$G$
-map with respect to the natural
![]() $G$
-action on
$G$
-action on
![]() $[V]^2$
induced by the
$[V]^2$
induced by the
![]() $G$
-set
$G$
-set
![]() $V$
. A morphism
$V$
. A morphism
![]() $(\phi _0,\phi _1)$
of
$(\phi _0,\phi _1)$
of
![]() $G$
-graphs is a morphism of graphs such that each
$G$
-graphs is a morphism of graphs such that each
![]() $\phi _i$
is a
$\phi _i$
is a
![]() $G$
-map. A
$G$
-map. A
![]() $G$
-equivariant embedding is a monomorphisms of
$G$
-equivariant embedding is a monomorphisms of
![]() $G$
-graphs. A
$G$
-graphs. A
![]() $G$
-action on a graph
$G$
-action on a graph
![]() $\Gamma$
has no inversions if for every
$\Gamma$
has no inversions if for every
![]() $e\in E$
and
$e\in E$
and
![]() $g\in G$
such that
$g\in G$
such that
![]() $g.e=e$
,
$g.e=e$
,
![]() $g.v=v$
for every
$g.v=v$
for every
![]() $v\in r(e)$
. For a
$v\in r(e)$
. For a
![]() $G$
-action without inversions on a graph
$G$
-action without inversions on a graph
![]() $\Gamma$
and
$\Gamma$
and
![]() $K\leq G$
, let
$K\leq G$
, let
![]() $\Gamma ^K$
denote subgraph of
$\Gamma ^K$
denote subgraph of
![]() $\Gamma$
defined by
$\Gamma$
defined by
![]() $V(\Gamma ^K) =\{v\in V(\Gamma )\mid k.v=v \text{ for all $k\in K$}\}$
and
$V(\Gamma ^K) =\{v\in V(\Gamma )\mid k.v=v \text{ for all $k\in K$}\}$
and
![]() $E(\Gamma ^K) =\{e\in E(\Gamma )\mid k.e=e \text{ for all $e\in K$}\}$
.
$E(\Gamma ^K) =\{e\in E(\Gamma )\mid k.e=e \text{ for all $e\in K$}\}$
.
4.4. Extending group actions on graphs
Let
![]() $K$
be a subgroup of
$K$
be a subgroup of
![]() $G$
, and let
$G$
, and let
![]() $\Lambda =(V,E,r)$
be a
$\Lambda =(V,E,r)$
be a
![]() $K$
-graph. Define
$K$
-graph. Define
where
![]() $\tilde r$
is unique
$\tilde r$
is unique
![]() $G$
-map induced by the commutative diagram
$G$
-map induced by the commutative diagram

where
![]() $\imath \;:\; V \hookrightarrow G\times _K V$
and
$\imath \;:\; V \hookrightarrow G\times _K V$
and
![]() $\jmath \;:\; E \hookrightarrow G\times _K E$
are the canonical
$\jmath \;:\; E \hookrightarrow G\times _K E$
are the canonical
![]() $K$
-maps, see Lemma 4.2(3). Note that there is a canonical
$K$
-maps, see Lemma 4.2(3). Note that there is a canonical
![]() $K$
-equivariant embedding
$K$
-equivariant embedding
induced by
![]() $\imath$
and
$\imath$
and
![]() $\jmath$
. We consider
$\jmath$
. We consider
![]() $\Lambda$
a
$\Lambda$
a
![]() $K$
-subgraph of
$K$
-subgraph of
![]() $G\times _K \Lambda$
.
$G\times _K \Lambda$
.
Remark 4.3. Proposition 4.2, parts 2 and 4 imply:
-
1. If
 $\Lambda$
is a simplicial
$\Lambda$
is a simplicial
 $K$
-graph without inversions, then
$K$
-graph without inversions, then
 $G\times _K\Lambda$
is a simplicial
$G\times _K\Lambda$
is a simplicial
 $G$
-graph without inversions.
$G$
-graph without inversions.
-
2. For any connected subgraph
 $\Delta$
of
$\Delta$
of
 $G\times _K \Lambda$
, there is
$G\times _K \Lambda$
, there is
 $g\in G$
such that
$g\in G$
such that
 $g.\Delta$
is a subcomplex of
$g.\Delta$
is a subcomplex of
 $\Lambda$
, in a commutative diagram,
$\Lambda$
, in a commutative diagram,

In particular, if
 $\Lambda$
is connected, then every connected component of
$\Lambda$
is connected, then every connected component of
 $G\times _K\Lambda$
is isomorphic to
$G\times _K\Lambda$
is isomorphic to
 $\Lambda$
.
$\Lambda$
.
4.5. Pushouts of graphs
Let
![]() $\mathsf X$
and
$\mathsf X$
and
![]() $\mathsf Y$
be
$\mathsf Y$
be
![]() $G$
-graphs, let
$G$
-graphs, let
![]() $C\leq G$
be a subgroup and suppose
$C\leq G$
be a subgroup and suppose
![]() $\mathsf X^C$
and
$\mathsf X^C$
and
![]() $\mathsf Y^C$
are nonempty. Let
$\mathsf Y^C$
are nonempty. Let
![]() $x\in \mathsf X^C$
and
$x\in \mathsf X^C$
and
![]() $y\in \mathsf Y^C$
be vertices. The
$y\in \mathsf Y^C$
be vertices. The
![]() $C$
-pushout
$C$
-pushout
![]() $\mathsf Z$
of
$\mathsf Z$
of
![]() $\mathsf X$
and
$\mathsf X$
and
![]() $\mathsf Y$
with respect to the pair
$\mathsf Y$
with respect to the pair
![]() $(x,y)$
is the
$(x,y)$
is the
![]() $G$
-graph
$G$
-graph
![]() $\mathsf Z$
obtained by taking the disjoint union of
$\mathsf Z$
obtained by taking the disjoint union of
![]() $\mathsf X$
and
$\mathsf X$
and
![]() $\mathsf Y$
and then identifying the vertex
$\mathsf Y$
and then identifying the vertex
![]() $g.x$
with the vertex
$g.x$
with the vertex
![]() $g.y$
for every
$g.y$
for every
![]() $g\in G$
.
$g\in G$
.
Equivalently, the
![]() $C$
-pushout
$C$
-pushout
![]() $\mathsf Z$
of
$\mathsf Z$
of
![]() $\mathsf X$
and
$\mathsf X$
and
![]() $\mathsf Y$
with respect to the pair
$\mathsf Y$
with respect to the pair
![]() $(x,y)$
is the
$(x,y)$
is the
![]() $G$
-graph
$G$
-graph
![]() $\mathsf Z$
whose vertex set
$\mathsf Z$
whose vertex set
![]() $V(Z)$
is the pushout of the
$V(Z)$
is the pushout of the
![]() $G$
-maps
$G$
-maps
![]() $\kappa _1\;:\; G/C\to \mathsf V(\mathsf X)$
and
$\kappa _1\;:\; G/C\to \mathsf V(\mathsf X)$
and
![]() $\kappa _2\;:\; G/C\to \mathsf V(\mathsf Y)$
given by
$\kappa _2\;:\; G/C\to \mathsf V(\mathsf Y)$
given by
![]() $C\mapsto x$
and
$C\mapsto x$
and
![]() $C\mapsto y$
; and edge set the disjoint union of the
$C\mapsto y$
; and edge set the disjoint union of the
![]() $G$
-sets
$G$
-sets
![]() $E(\mathsf X)$
and
$E(\mathsf X)$
and
![]() $E(\mathsf Y)$
, and attaching map
$E(\mathsf Y)$
, and attaching map
![]() $E(\mathsf Z) \to V(\mathsf Z)^2$
defined as the union of the attaching maps for
$E(\mathsf Z) \to V(\mathsf Z)^2$
defined as the union of the attaching maps for
![]() $\mathsf X$
and
$\mathsf X$
and
![]() $\mathsf Y$
postcomposed with the maps
$\mathsf Y$
postcomposed with the maps
![]() $V(\mathsf X) \to V(\mathsf Z)$
and
$V(\mathsf X) \to V(\mathsf Z)$
and
![]() $V(\mathsf Y) \to V(\mathsf Z)$
defining the pushout.
$V(\mathsf Y) \to V(\mathsf Z)$
defining the pushout.

The standard universal property of pushouts holds for this construction: if
![]() $\jmath _1\;:\; \mathsf X \to \mathsf W$
and
$\jmath _1\;:\; \mathsf X \to \mathsf W$
and
![]() $\jmath _2\;:\; \mathsf Y \to \mathsf W$
are morphisms of
$\jmath _2\;:\; \mathsf Y \to \mathsf W$
are morphisms of
![]() $G$
-graphs such that
$G$
-graphs such that
![]() $\jmath _1\circ \kappa _1 = \jmath _2\circ \kappa _2$
, then there is a unique morphism of
$\jmath _1\circ \kappa _1 = \jmath _2\circ \kappa _2$
, then there is a unique morphism of
![]() $G$
-graphs
$G$
-graphs
![]() $\mathsf Z\to \mathsf W$
such that above diagram commutes.
$\mathsf Z\to \mathsf W$
such that above diagram commutes.
Remark 4.4.
Let
![]() $\mathsf Z$
be the
$\mathsf Z$
be the
![]() $C$
-pushout of
$C$
-pushout of
![]() $\mathsf X$
and
$\mathsf X$
and
![]() $\mathsf Y$
with respect to a pair
$\mathsf Y$
with respect to a pair
![]() $(x,y)$
.
$(x,y)$
.
-
1. For any vertex
 $x$
in
$x$
in
 $\mathsf X$
,
$\mathsf X$
,
 $G_x = G_{\imath _1(x)}$
or
$G_x = G_{\imath _1(x)}$
or
 $x$
is in the image of
$x$
is in the image of
 $\kappa _1$
.
$\kappa _1$
. -
2. For any edge
 $e$
of
$e$
of
 $X$
,
$X$
,
 $G_e = G_{\imath _1(e)}$
.
$G_e = G_{\imath _1(e)}$
. -
3. If
 $\mathsf X/ G$
and
$\mathsf X/ G$
and
 $\mathsf Y/ G$
both have finitely many vertices (resp. edges), then
$\mathsf Y/ G$
both have finitely many vertices (resp. edges), then
 $\mathsf Z/ G$
has finitely many vertices (resp. edges).
$\mathsf Z/ G$
has finitely many vertices (resp. edges).
Example 4.1.
Let
![]() $G=A\ast _C B$
where
$G=A\ast _C B$
where
![]() $A$
and
$A$
and
![]() $B$
are free abelian groups of rank two, and
$B$
are free abelian groups of rank two, and
![]() $C$
is maximal cyclic subgroup of
$C$
is maximal cyclic subgroup of
![]() $A$
and
$A$
and
![]() $B$
. Let
$B$
. Let
![]() $\mathsf X$
be the
$\mathsf X$
be the
![]() $A$
-graph consisting of a single vertex with the trivial
$A$
-graph consisting of a single vertex with the trivial
![]() $A$
-action and define
$A$
-action and define
![]() $\mathsf Y$
analogously for
$\mathsf Y$
analogously for
![]() $B$
. Then the graph
$B$
. Then the graph
![]() $G\times _{A} \mathsf X$
is the edgeless
$G\times _{A} \mathsf X$
is the edgeless
![]() $G$
-graph with vertex set the collection of left cosets of
$G$
-graph with vertex set the collection of left cosets of
![]() $G/A$
; and analogously
$G/A$
; and analogously
![]() $G\times _{B} Y$
is the edgeless graph with vertex set
$G\times _{B} Y$
is the edgeless graph with vertex set
![]() $G/B$
. Let
$G/B$
. Let
![]() $\mathsf Z$
be the
$\mathsf Z$
be the
![]() $C$
-pushout of
$C$
-pushout of
![]() $\mathsf X$
and
$\mathsf X$
and
![]() $\mathsf Y$
. By parts (4) and (7) of Proposition 4.5,
$\mathsf Y$
. By parts (4) and (7) of Proposition 4.5,
![]() $\mathsf Z$
is a connected edgeless
$\mathsf Z$
is a connected edgeless
![]() $G$
-graph and hence a single vertex.
$G$
-graph and hence a single vertex.
Example 4.2.
Let
![]() $A=\langle a_1,a_2,a_3\mid [a_1,a_2] \rangle$
and
$A=\langle a_1,a_2,a_3\mid [a_1,a_2] \rangle$
and
![]() $B=\langle b_1,b_2,b_3\mid [b_1,b_2] \rangle$
, and let
$B=\langle b_1,b_2,b_3\mid [b_1,b_2] \rangle$
, and let
![]() $\mathsf X=\hat \Gamma (A,\langle a_1,a_2 \rangle, a_3)$
and
$\mathsf X=\hat \Gamma (A,\langle a_1,a_2 \rangle, a_3)$
and
![]() $\mathsf Y=\hat \Gamma (B,\langle b_1,b_2 \rangle, b_3)$
be the coned-off Cayley graphs. Note that
$\mathsf Y=\hat \Gamma (B,\langle b_1,b_2 \rangle, b_3)$
be the coned-off Cayley graphs. Note that
![]() $\mathsf X$
is the Bass–Serre tree of the splitting of
$\mathsf X$
is the Bass–Serre tree of the splitting of
![]() $A$
as the graph of groups
$A$
as the graph of groups

with two vertices and two edges with trivial edge group.
Let
![]() $G=A\ast _C B$
be the amalgamated product where
$G=A\ast _C B$
be the amalgamated product where
![]() $C$
corresponds to the cyclic subgroup
$C$
corresponds to the cyclic subgroup
![]() $\langle a_1 \rangle \leq A$
and
$\langle a_1 \rangle \leq A$
and
![]() $\langle b_1 \rangle \leq B$
. Consider the
$\langle b_1 \rangle \leq B$
. Consider the
![]() $C$
-pushout
$C$
-pushout
![]() $\mathsf Z$
of
$\mathsf Z$
of
![]() $G\times _A \mathsf X$
and
$G\times _A \mathsf X$
and
![]() $G\times _B \mathsf Y$
. By the fourth, fifth and sixth statements of Proposition 4.5 below,
$G\times _B \mathsf Y$
. By the fourth, fifth and sixth statements of Proposition 4.5 below,
![]() $\mathsf Z$
is a tree, it contains three distinct
$\mathsf Z$
is a tree, it contains three distinct
![]() $G$
-orbits of vertices, two of these
$G$
-orbits of vertices, two of these
![]() $G$
-orbits have all representatives with trivial stabilizer, and there is a vertex
$G$
-orbits have all representatives with trivial stabilizer, and there is a vertex
![]() $z$
with stabilizer
$z$
with stabilizer
![]() $\langle a_1, a_2, b_2\rangle = \langle a_1, a_2\rangle \ast _{\langle a_1 \rangle =\langle b_1 \rangle } \langle b_1, b_2 \rangle$
, and there are four distinct orbits of edges all with representatives having trivial stabilizer. Hence,
$\langle a_1, a_2, b_2\rangle = \langle a_1, a_2\rangle \ast _{\langle a_1 \rangle =\langle b_1 \rangle } \langle b_1, b_2 \rangle$
, and there are four distinct orbits of edges all with representatives having trivial stabilizer. Hence,
![]() $\mathsf Z$
is the Bass-Serre tree of a splitting of
$\mathsf Z$
is the Bass-Serre tree of a splitting of
![]() $G$
given by the graph of groups
$G$
given by the graph of groups

with three vertices and four edges. In particular,
![]() $Z$
is the coned-off Cayley graph of
$Z$
is the coned-off Cayley graph of
![]() $\hat \Gamma (G, G_y, \{a_3,b_3\})$
.
$\hat \Gamma (G, G_y, \{a_3,b_3\})$
.
Proposition 4.5.
Let
![]() $G$
be the amalgamated free product group
$G$
be the amalgamated free product group
![]() $A\ast _C B$
, let
$A\ast _C B$
, let
![]() $\mathsf{X}$
be a
$\mathsf{X}$
be a
![]() $A$
-graph, and let
$A$
-graph, and let
![]() $\mathsf{Y}$
be a
$\mathsf{Y}$
be a
![]() $B$
-graph. Let
$B$
-graph. Let
![]() $x\in \mathsf{X}^C$
and
$x\in \mathsf{X}^C$
and
![]() $y\in \mathsf{Y}^C$
be vertices. Let
$y\in \mathsf{Y}^C$
be vertices. Let
![]() $\mathsf{Z}$
be the
$\mathsf{Z}$
be the
![]() $C$
-pushout of
$C$
-pushout of
![]() $G\times _{A} \mathsf{X}$
and
$G\times _{A} \mathsf{X}$
and
![]() $G\times _{B} \mathsf{Y}$
with respect to
$G\times _{B} \mathsf{Y}$
with respect to
![]() $( x, y)$
. Let
$( x, y)$
. Let
![]() $z=\imath _1(x)=\imath _2(y)$
. The following properties hold:
$z=\imath _1(x)=\imath _2(y)$
. The following properties hold:
-
1. The homomorphism
 $A_x \ast _C B_y \to G$
induced by the inclusions
$A_x \ast _C B_y \to G$
induced by the inclusions
 $A_x\leq G$
and
$A_x\leq G$
and
 $B_y\leq G$
is injective and has image
$B_y\leq G$
is injective and has image
 $G_z$
. In particular,
$G_z$
. In particular,
 $G_z=\langle A_x, B_y \rangle$
is isomorphic to
$G_z=\langle A_x, B_y \rangle$
is isomorphic to
 $A_x \ast _C B_y$
.
$A_x \ast _C B_y$
. -
2. The morphism
 $\mathsf{X}\hookrightarrow G\times _A \mathsf{X} \xrightarrow{\imath _1} \mathsf{Z}$
is an
$\mathsf{X}\hookrightarrow G\times _A \mathsf{X} \xrightarrow{\imath _1} \mathsf{Z}$
is an
 $A$
-equivariant embedding. Analogously,
$A$
-equivariant embedding. Analogously,
 $\mathsf{Y}\hookrightarrow G\times _B \mathsf{Y} \xrightarrow{\imath _2} \mathsf{Z}$
is a
$\mathsf{Y}\hookrightarrow G\times _B \mathsf{Y} \xrightarrow{\imath _2} \mathsf{Z}$
is a
 $B$
-equivariant embedding.
$B$
-equivariant embedding.
-
From here on, we consider
 $\mathsf X$
and
$\mathsf X$
and
 $\mathsf Y$
as subgraphs of
$\mathsf Y$
as subgraphs of
 $\mathsf Z$
via these canonical embeddings.
$\mathsf Z$
via these canonical embeddings.
-
3. For every vertex
 $v$
(resp. edge
$v$
(resp. edge
 $e$
) of
$e$
) of
 $\mathsf Z$
, there is
$\mathsf Z$
, there is
 $g\in G$
such that
$g\in G$
such that
 $g.v$
is a vertex (resp. is an edge
$g.v$
is a vertex (resp. is an edge
 $g.e$
) of the subgraph
$g.e$
) of the subgraph
 $\mathsf X \cup \mathsf{Y}$
.
$\mathsf X \cup \mathsf{Y}$
. -
4. For every vertex
 $v$
of
$v$
of
 $\mathsf{X}$
which is not in the
$\mathsf{X}$
which is not in the
 $A$
-orbit of
$A$
-orbit of
 $x$
,
$x$
,
 $A_v = G_v$
where
$A_v = G_v$
where
 $G_v$
is the
$G_v$
is the
 $G$
-stabilizer of
$G$
-stabilizer of
 $v$
in
$v$
in
 $\mathsf Z$
. Analogously for every vertex
$\mathsf Z$
. Analogously for every vertex
 $v$
of
$v$
of
 $\mathsf{Y}$
not in the
$\mathsf{Y}$
not in the
 $B$
-orbit of
$B$
-orbit of
 $y$
,
$y$
,
 $B_v=G_v$
.
$B_v=G_v$
. -
5. For every edge
 $e$
of
$e$
of
 $\mathsf X$
(resp.
$\mathsf X$
(resp.
 $\mathsf Y$
),
$\mathsf Y$
),
 $A_e=G_e$
(resp.
$A_e=G_e$
(resp.
 $B_e=G_e$
) where
$B_e=G_e$
) where
 $G_e$
is the
$G_e$
is the
 $G$
-stabilizer of
$G$
-stabilizer of
 $e$
in
$e$
in
 $\mathsf Z$
.
$\mathsf Z$
. -
6. If the complexes
 $\mathsf X/ A$
and
$\mathsf X/ A$
and
 $\mathsf Y/ B$
both have finitely many vertices (resp. edges), then
$\mathsf Y/ B$
both have finitely many vertices (resp. edges), then
 $\mathsf Z/ G$
has finitely many vertices (resp. edges).
$\mathsf Z/ G$
has finitely many vertices (resp. edges).
-
7. If
 $\mathsf{X}$
and
$\mathsf{X}$
and
 $\mathsf{Y}$
are connected, then
$\mathsf{Y}$
are connected, then
 $\mathsf{Z}$
is connected.
$\mathsf{Z}$
is connected.
-
8. There is a
 $G$
-tree
$G$
-tree
 $T$
and a morphism
$T$
and a morphism
 $\xi \;:\; \mathsf Z \to T$
of
$\xi \;:\; \mathsf Z \to T$
of
 $G$
-graphs with the following properties: The
$G$
-graphs with the following properties: The
 $G$
-orbit of
$G$
-orbit of
 $\xi (z)$
and its complement in the set of vertices of
$\xi (z)$
and its complement in the set of vertices of
 $T$
make
$T$
make
 $T$
a bipartite graph; the preimage
$T$
a bipartite graph; the preimage
 $\xi ^{-1}(\xi (z))$
is a single vertex; and if a vertex
$\xi ^{-1}(\xi (z))$
is a single vertex; and if a vertex
 $v$
of
$v$
of
 $T$
is not in the
$T$
is not in the
 $G$
-orbit of
$G$
-orbit of
 $\xi (z)$
, then the preimage of the star of
$\xi (z)$
, then the preimage of the star of
 $v$
is a subgraph of
$v$
is a subgraph of
 $\mathsf Z$
isomorphic to
$\mathsf Z$
isomorphic to
 $\mathsf X$
or
$\mathsf X$
or
 $\mathsf Y$
.
$\mathsf Y$
.
Proof. The first item is a direct consequence of Proposition 4.1. For the second item, first note that that the composition
![]() $\mathsf X\hookrightarrow G\times _A \mathsf X \xrightarrow{\imath _{1}} \mathsf Z$
is a morphism of
$\mathsf X\hookrightarrow G\times _A \mathsf X \xrightarrow{\imath _{1}} \mathsf Z$
is a morphism of
![]() $A$
-graphs. Observe that to prove the embedding part is enough to consider only vertices of
$A$
-graphs. Observe that to prove the embedding part is enough to consider only vertices of
![]() $\mathsf X$
that are in the
$\mathsf X$
that are in the
![]() $A$
-orbit of
$A$
-orbit of
![]() $x$
. Suppose that
$x$
. Suppose that
![]() $a.x$
and
$a.x$
and
![]() $x$
with
$x$
with
![]() $a\in A$
both map to
$a\in A$
both map to
![]() $z \in \mathsf Z$
. Then,
$z \in \mathsf Z$
. Then,
![]() $a \in G_{z} = A_{x} \ast _C B_y$
and therefore
$a \in G_{z} = A_{x} \ast _C B_y$
and therefore
![]() $a\in A_x$
and hence
$a\in A_x$
and hence
![]() $a.x=x$
. Item three follows directly from the definition of
$a.x=x$
. Item three follows directly from the definition of
![]() $\mathsf Z$
, and items four to six are consequences of Proposition 4.2.
$\mathsf Z$
, and items four to six are consequences of Proposition 4.2.
To prove the seventh statement suppose that
![]() $X$
and
$X$
and
![]() $Y$
are connected graphs. The subgraph
$Y$
are connected graphs. The subgraph
![]() $\mathsf X\cup \mathsf Y$
of
$\mathsf X\cup \mathsf Y$
of
![]() $\mathsf Z$
is connected since both
$\mathsf Z$
is connected since both
![]() $\mathsf X$
and
$\mathsf X$
and
![]() $\mathsf Y$
contain the vertex
$\mathsf Y$
contain the vertex
![]() $z$
. On the other hand, any vertex of
$z$
. On the other hand, any vertex of
![]() $\mathsf Z$
belongs to a translate of
$\mathsf Z$
belongs to a translate of
![]() $\mathsf X \cup \mathsf Y$
by an element of
$\mathsf X \cup \mathsf Y$
by an element of
![]() $G$
. Therefore to prove that
$G$
. Therefore to prove that
![]() $\mathsf Z$
is connected, it is enough to show that for any
$\mathsf Z$
is connected, it is enough to show that for any
![]() $g\in G$
there is a path in
$g\in G$
there is a path in
![]() $\mathsf Z$
from
$\mathsf Z$
from
![]() $z$
to
$z$
to
![]() $g.z$
. For any
$g.z$
. For any
![]() $g\in G$
and
$g\in G$
and
![]() $a\in A$
, there is a path from
$a\in A$
, there is a path from
![]() $g.z$
to
$g.z$
to
![]() $ga.z$
in
$ga.z$
in
![]() $\mathsf Z$
: indeed, there is a path from
$\mathsf Z$
: indeed, there is a path from
![]() $z$
to
$z$
to
![]() $a.z$
in the connected
$a.z$
in the connected
![]() $A$
-subgraph
$A$
-subgraph
![]() $\mathsf X$
of
$\mathsf X$
of
![]() $\mathsf Z$
, and hence there is a path from
$\mathsf Z$
, and hence there is a path from
![]() $g.z$
to
$g.z$
to
![]() $ga.z$
in
$ga.z$
in
![]() $\mathsf Z$
. Analogously, for any
$\mathsf Z$
. Analogously, for any
![]() $g\in G$
and
$g\in G$
and
![]() $b\in B$
, there is a path from
$b\in B$
, there is a path from
![]() $g.z$
to
$g.z$
to
![]() $gb.z$
. Since any element of
$gb.z$
. Since any element of
![]() $G$
is of the form
$G$
is of the form
![]() $a_1b_1\ldots a_nb_n$
with
$a_1b_1\ldots a_nb_n$
with
![]() $a_i\in A$
and
$a_i\in A$
and
![]() $b_i \in B$
, there is a path from
$b_i \in B$
, there is a path from
![]() $z$
to
$z$
to
![]() $g.z$
for any
$g.z$
for any
![]() $g\in G$
.
$g\in G$
.
Now we prove the eighth statement. Observe that
![]() $G$
splits as
$G$
splits as
![]() $G=A\ast _{A_x}(A_x\ast _CB_y)\ast _{B_y}B$
where the subgroups
$G=A\ast _{A_x}(A_x\ast _CB_y)\ast _{B_y}B$
where the subgroups
![]() $A_x$
,
$A_x$
,
![]() $B_y$
and
$B_y$
and
![]() $A_x\ast _C B_y$
are naturally identified with the
$A_x\ast _C B_y$
are naturally identified with the
![]() $G$
-stabilizers of
$G$
-stabilizers of
![]() $x\in G\times _A \mathsf X$
,
$x\in G\times _A \mathsf X$
,
![]() $y\in G\times _B \mathsf Y$
, and
$y\in G\times _B \mathsf Y$
, and
![]() $z\in \mathsf Z$
. Let
$z\in \mathsf Z$
. Let
![]() $T$
denote the Bass–Serre tree of this splitting. The vertex and edge sets of
$T$
denote the Bass–Serre tree of this splitting. The vertex and edge sets of
![]() $T$
can be described as:
$T$
can be described as:
and
respectively. Note that
![]() $T$
is a bipartite
$T$
is a bipartite
![]() $G$
-graph, the equivariant bipartition of the vertices given by
$G$
-graph, the equivariant bipartition of the vertices given by
![]() $G/A\sqcup G/B$
and
$G/A\sqcup G/B$
and
![]() $G/(A_x\ast _CB_y)$
.
$G/(A_x\ast _CB_y)$
.
Consider the
![]() $A$
-map from
$A$
-map from
![]() $\mathsf X$
to
$\mathsf X$
to
![]() $T$
that maps every vertex of
$T$
that maps every vertex of
![]() $\mathsf X$
not in the
$\mathsf X$
not in the
![]() $A$
-orbit of
$A$
-orbit of
![]() $x$
to the vertex
$x$
to the vertex
![]() $A$
, and
$A$
, and
![]() $x\mapsto A_x\ast _C B_y$
. Since
$x\mapsto A_x\ast _C B_y$
. Since
![]() $T$
is simplicial, this induces a unique morphism of
$T$
is simplicial, this induces a unique morphism of
![]() $G$
-graphs
$G$
-graphs
![]() $\jmath _1\;:\; G\times _A \mathsf X \to T$
. Analogously, there is
$\jmath _1\;:\; G\times _A \mathsf X \to T$
. Analogously, there is
![]() $B$
-map
$B$
-map
![]() $\mathsf Y\to T$
that maps every vertex not in the
$\mathsf Y\to T$
that maps every vertex not in the
![]() $B$
-orbit of
$B$
-orbit of
![]() $y$
to the vertex
$y$
to the vertex
![]() $B$
and
$B$
and
![]() $y\mapsto A_x\ast _C B_y$
; this induces a unique
$y\mapsto A_x\ast _C B_y$
; this induces a unique
![]() $G$
-map
$G$
-map
![]() $\jmath _2\;:\; G\times _B \mathsf Y \to T$
.
$\jmath _2\;:\; G\times _B \mathsf Y \to T$
.

Consider the
![]() $G$
-maps
$G$
-maps
![]() $\kappa _1 \;:\; G/C \to G\times _A \mathsf X$
and
$\kappa _1 \;:\; G/C \to G\times _A \mathsf X$
and
![]() $\kappa _2\;:\; G/C \to G\times _B \mathsf Y$
given by
$\kappa _2\;:\; G/C \to G\times _B \mathsf Y$
given by
![]() $C\mapsto x$
and
$C\mapsto x$
and
![]() $C\mapsto y$
, respectively. Since
$C\mapsto y$
, respectively. Since
![]() $\jmath _1\circ \kappa _1 = \jmath _2\circ \kappa _2$
, the universal property implies that there is a surjective
$\jmath _1\circ \kappa _1 = \jmath _2\circ \kappa _2$
, the universal property implies that there is a surjective
![]() $G$
-map
$G$
-map
![]() $\xi \;:\; \mathsf Z\to T$
.
$\xi \;:\; \mathsf Z\to T$
.
Note that
![]() $\xi ^{-1}(\xi (z))$
is contained in the orbit
$\xi ^{-1}(\xi (z))$
is contained in the orbit
![]() $G.z$
. Suppose
$G.z$
. Suppose
![]() $g.z\in \xi ^{-1}(\xi (z))$
. Then
$g.z\in \xi ^{-1}(\xi (z))$
. Then
![]() $g(A_x\ast _C B_y) = A_x\ast _C B_y$
and hence
$g(A_x\ast _C B_y) = A_x\ast _C B_y$
and hence
![]() $g\in A_x\ast _C B_y$
. Since
$g\in A_x\ast _C B_y$
. Since
![]() $A_x\ast _C B_y$
is the
$A_x\ast _C B_y$
is the
![]() $G$
-stabilizer of
$G$
-stabilizer of
![]() $z$
, we have that
$z$
, we have that
![]() $g.z=z$
. This shows that
$g.z=z$
. This shows that
![]() $\xi ^{-1}(\xi (z))=\{z\}$
.
$\xi ^{-1}(\xi (z))=\{z\}$
.
Let us conclude by proving that if
![]() $v\in V(T)$
is not in the
$v\in V(T)$
is not in the
![]() $G$
-orbit of
$G$
-orbit of
![]() $\xi (z)=A_x\ast _c B_y$
then
$\xi (z)=A_x\ast _c B_y$
then
![]() $\xi ^{-1}(\mathsf{star_T}(v))$
is a graph isomorphic to either
$\xi ^{-1}(\mathsf{star_T}(v))$
is a graph isomorphic to either
![]() $\mathsf X$
or
$\mathsf X$
or
![]() $\mathsf{Y}$
. Note that such a vertex
$\mathsf{Y}$
. Note that such a vertex
![]() $v$
is an element of
$v$
is an element of
![]() $G/A \cup G/B$
. By equivariance, it is enough to consider the two symmetric cases, namely
$G/A \cup G/B$
. By equivariance, it is enough to consider the two symmetric cases, namely
![]() $v=A$
or
$v=A$
or
![]() $v=B$
. Let us prove that
$v=B$
. Let us prove that
![]() $\xi ^{-1}(\mathsf{star}_T{A})$
is isomorphic to
$\xi ^{-1}(\mathsf{star}_T{A})$
is isomorphic to
![]() $\mathsf X$
. Observe that any edge of
$\mathsf X$
. Observe that any edge of
![]() $\mathsf{star}_T(A)$
is of the form
$\mathsf{star}_T(A)$
is of the form
![]() $\{A, a(A_x\ast _C B_y)\}$
with
$\{A, a(A_x\ast _C B_y)\}$
with
![]() $a\in A$
. Since
$a\in A$
. Since
![]() $(\xi \circ \imath _1)^{-1}(\mathsf{star}_T(A)) = \jmath _1^{-1}(\mathsf{star}_T(A))$
and
$(\xi \circ \imath _1)^{-1}(\mathsf{star}_T(A)) = \jmath _1^{-1}(\mathsf{star}_T(A))$
and
![]() $\xi ^{-1}(\mathsf{star}_T(A)) \subset \imath _1(G\times _A X)$
, we have that
$\xi ^{-1}(\mathsf{star}_T(A)) \subset \imath _1(G\times _A X)$
, we have that
![]() $\xi ^{-1}(\mathsf{star}_T(A)) = \imath _1(\jmath _1^{-1}(\mathsf{star}_T(A))$
. Recall that the canonical
$\xi ^{-1}(\mathsf{star}_T(A)) = \imath _1(\jmath _1^{-1}(\mathsf{star}_T(A))$
. Recall that the canonical
![]() $A$
-map
$A$
-map
![]() $\mathsf{X} \to G\times _A \mathsf{X}$
is injective, and this defines a natural identification of
$\mathsf{X} \to G\times _A \mathsf{X}$
is injective, and this defines a natural identification of
![]() $\mathsf{X}$
with a subgraph of
$\mathsf{X}$
with a subgraph of
![]() $G\times _A \mathsf{X}$
which equals
$G\times _A \mathsf{X}$
which equals
![]() $\jmath ^{-1}(\mathsf{star}_T(A))$
by definition of
$\jmath ^{-1}(\mathsf{star}_T(A))$
by definition of
![]() $\jmath$
. Then we have that
$\jmath$
. Then we have that
![]() $\imath _1(\jmath _1^{-1}(\mathsf{star}_T(A))=\imath _1(\mathsf{X})$
is isomorphic to
$\imath _1(\jmath _1^{-1}(\mathsf{star}_T(A))=\imath _1(\mathsf{X})$
is isomorphic to
![]() $\mathsf X$
by the second item of the proposition.
$\mathsf X$
by the second item of the proposition.
4.6. Proof of Theorem 3.1
Lemma 4.6.
Let
![]() $\xi \;:\; \Gamma \to T$
be a morphism of graphs where
$\xi \;:\; \Gamma \to T$
be a morphism of graphs where
![]() $T$
is a bipartite tree, say
$T$
is a bipartite tree, say
![]() $V(T)=K \cup L$
. Suppose
$V(T)=K \cup L$
. Suppose
![]() $\xi ^{-1}(v)$
is a single vertex for every
$\xi ^{-1}(v)$
is a single vertex for every
![]() $v\in L$
, and
$v\in L$
, and
![]() $\xi ^{-1}(\mathsf{star}(v))$
is a connected subgraph for every
$\xi ^{-1}(\mathsf{star}(v))$
is a connected subgraph for every
![]() $v\in K$
. Let
$v\in K$
. Let
![]() $\Omega = \{ \xi ^{-1}(\mathsf{star}(v)) \mid v\in K \}$
. Then:
$\Omega = \{ \xi ^{-1}(\mathsf{star}(v)) \mid v\in K \}$
. Then:
-
1.
 $\Gamma$
is a simplicial graph if and only if every
$\Gamma$
is a simplicial graph if and only if every
 $\Delta \in \Omega$
is simplicial.
$\Delta \in \Omega$
is simplicial.
-
2.
 $\Gamma$
is a
$\Gamma$
is a
 $\delta$
-hyperbolic graph if and only if every
$\delta$
-hyperbolic graph if and only if every
 $\Delta \in \Omega$
is a
$\Delta \in \Omega$
is a
 $\delta$
-hyperbolic graph.
$\delta$
-hyperbolic graph.
-
3. For any vertex
 $u$
of
$u$
of
 $\Gamma$
, the following statements are equivalent:
$\Gamma$
, the following statements are equivalent:
-
•
 $\Gamma$
is fine at
$\Gamma$
is fine at
 $u$
.
$u$
. -
• For every
 $\Delta \in \Omega$
, if
$\Delta \in \Omega$
, if
 $u$
is a vertex of
$u$
is a vertex of
 $\Delta$
, then
$\Delta$
, then
 $\Delta$
is fine at
$\Delta$
is fine at
 $u$
.
$u$
.
-
Proof. Note for any vertex
![]() $u$
of
$u$
of
![]() $\Gamma$
, if
$\Gamma$
, if
![]() $\xi (u)\in L$
then
$\xi (u)\in L$
then
![]() $u$
is a cut vertex of
$u$
is a cut vertex of
![]() $\Gamma$
. The bipartite assumption on
$\Gamma$
. The bipartite assumption on
![]() $T$
implies that if
$T$
implies that if
![]() $\Theta$
is the closure of a connected component of
$\Theta$
is the closure of a connected component of
![]() $\Gamma \setminus \xi ^{-1}(L)$
, then
$\Gamma \setminus \xi ^{-1}(L)$
, then
![]() $\Theta$
equals some
$\Theta$
equals some
![]() $\Delta \in \Omega$
.
$\Delta \in \Omega$
.
The first and second statements follow from the previous observation, the second one with important generalizations [Reference Bestvina and Feighn3]. For the third statement, if
![]() $\Gamma$
is fine at
$\Gamma$
is fine at
![]() $u$
, then any subgraph containing
$u$
, then any subgraph containing
![]() $u$
is fine at
$u$
is fine at
![]() $u$
. Conversely, let
$u$
. Conversely, let
![]() $u$
be a vertex of
$u$
be a vertex of
![]() $\Gamma$
such that any
$\Gamma$
such that any
![]() $\Delta$
containing
$\Delta$
containing
![]() $u$
is fine at
$u$
is fine at
![]() $u$
. There are two cases to consider.
$u$
. There are two cases to consider.
Suppose that
![]() $\xi (u) \in K$
. Then there is a unique
$\xi (u) \in K$
. Then there is a unique
![]() $\Delta \in \Omega$
that contains
$\Delta \in \Omega$
that contains
![]() $u$
. The bipartite assumption implies that
$u$
. The bipartite assumption implies that
![]() $T_u \Delta = T_u\Gamma$
. Since every vertex of
$T_u \Delta = T_u\Gamma$
. Since every vertex of
![]() $\Gamma$
that maps to
$\Gamma$
that maps to
![]() $L$
disconnects
$L$
disconnects
![]() $\Gamma$
, the metric spaces
$\Gamma$
, the metric spaces
![]() $(T_u \Delta, \angle _u)$
and
$(T_u \Delta, \angle _u)$
and
![]() $(T_u \Gamma, \angle _u)$
coincide. Since
$(T_u \Gamma, \angle _u)$
coincide. Since
![]() $\Delta$
is fine at
$\Delta$
is fine at
![]() $u$
, then
$u$
, then
![]() $\Gamma$
is fine at
$\Gamma$
is fine at
![]() $u$
.
$u$
.
Suppose that
![]() $\xi (u)\in L$
. Observe if
$\xi (u)\in L$
. Observe if
![]() $x,y\in T_u\Gamma$
and
$x,y\in T_u\Gamma$
and
![]() $x$
and
$x$
and
![]() $y$
belong to different subgraphs in
$y$
belong to different subgraphs in
![]() $\Omega$
, then
$\Omega$
, then
![]() $\angle _u(x,y)=\infty$
. Therefore, for any
$\angle _u(x,y)=\infty$
. Therefore, for any
![]() $x\in T_u\Gamma$
, every ball of finite radius in
$x\in T_u\Gamma$
, every ball of finite radius in
![]() $T_u\Gamma$
centered at
$T_u\Gamma$
centered at
![]() $x$
is a ball of finite radius in
$x$
is a ball of finite radius in
![]() $T_u \Delta$
centered at
$T_u \Delta$
centered at
![]() $x$
for some
$x$
for some
![]() $\Delta$
. Since by assumption,
$\Delta$
. Since by assumption,
![]() $\Delta$
is fine at
$\Delta$
is fine at
![]() $v$
, every ball of finite radius in
$v$
, every ball of finite radius in
![]() $T_v\Gamma$
centered at
$T_v\Gamma$
centered at
![]() $x$
is finite.
$x$
is finite.
Proof of Theorem 3.1. Let
![]() $\Gamma$
be the
$\Gamma$
be the
![]() $C$
-pushout of the
$C$
-pushout of the
![]() $G$
-graphs
$G$
-graphs
![]() $G\times _{G_1} \Gamma _1$
and
$G\times _{G_1} \Gamma _1$
and
![]() $G\times _{G_2} \Gamma _2$
with respect to
$G\times _{G_2} \Gamma _2$
with respect to
![]() $(x_1,x_2)$
, and let
$(x_1,x_2)$
, and let
![]() $z$
be the image of
$z$
be the image of
![]() $x_1$
in
$x_1$
in
![]() $\Gamma$
. The first six properties of
$\Gamma$
. The first six properties of
![]() $\Gamma$
are direct corollaries of Proposition 4.5. The last four properties follow directly by invoking Proposition 4.5(8) and Lemma 4.6.
$\Gamma$
are direct corollaries of Proposition 4.5. The last four properties follow directly by invoking Proposition 4.5(8) and Lemma 4.6.
5. HNN-extensions
This section describes a proof of Theorem 3.2. The argument is analogous to the one proving Theorem 3.1. In this case, we need to construct a
![]() $G\ast _\varphi$
-graph from a given
$G\ast _\varphi$
-graph from a given
![]() $G$
-graph that we call the
$G$
-graph that we call the
![]() $\varphi$
-coalescence.
$\varphi$
-coalescence.
Definition 5.1 (Coalescence in sets). Let
![]() $H$
be a subgroup of a group
$H$
be a subgroup of a group
![]() $A$
, let
$A$
, let
![]() $\varphi \;:\; H\to A$
be a monomorphism and let
$\varphi \;:\; H\to A$
be a monomorphism and let
![]() $G$
be the HNN-extension:
$G$
be the HNN-extension:
Let
![]() $ X$
be an
$ X$
be an
![]() $A$
-set,
$A$
-set,
![]() $x\in X^H$
and
$x\in X^H$
and
![]() $y\in X^{\varphi (H)}$
. The
$y\in X^{\varphi (H)}$
. The
![]() $\varphi$
-coalescence of
$\varphi$
-coalescence of
![]() $X$
with respect to
$X$
with respect to
![]() $(x,y)$
is the
$(x,y)$
is the
![]() $G$
-set
$G$
-set
![]() $Z$
arising as quotient of
$Z$
arising as quotient of
![]() $G\times _A X$
by the equivalence relation generated by the set of basic relations:
$G\times _A X$
by the equivalence relation generated by the set of basic relations:
Note that the quotient map:
is
![]() $G$
-equivariant.
$G$
-equivariant.
Example 5.1.
Let
![]() $\varphi \;:\; A\to A$
be a group automorphism and consider the HNN-extension
$\varphi \;:\; A\to A$
be a group automorphism and consider the HNN-extension
![]() $G=A\ast _\varphi$
. Let
$G=A\ast _\varphi$
. Let
![]() $X$
be the
$X$
be the
![]() $A$
-set consisting of a single point. Then
$A$
-set consisting of a single point. Then
![]() $G\times _A X$
is the
$G\times _A X$
is the
![]() $G$
-space
$G$
-space
![]() $G/A$
, and then the
$G/A$
, and then the
![]() $\varphi$
-coalescence of
$\varphi$
-coalescence of
![]() $X$
is again a single point.
$X$
is again a single point.
Example 5.2.
Consider a free product
![]() $A=H_1\ast H_2$
. Let
$A=H_1\ast H_2$
. Let
![]() $\varphi \;:\; H_1 \to H_2$
be an isomorphism, and
$\varphi \;:\; H_1 \to H_2$
be an isomorphism, and
![]() $G=A\ast _\varphi$
. Let
$G=A\ast _\varphi$
. Let
![]() $X$
be the
$X$
be the
![]() $A$
-set
$A$
-set
![]() $A/H_1 \cup A/H_2$
of all left cosets of
$A/H_1 \cup A/H_2$
of all left cosets of
![]() $H_1$
and
$H_1$
and
![]() $H_2$
in
$H_2$
in
![]() $A$
. Then
$A$
. Then
![]() $G\times _A X$
is the
$G\times _A X$
is the
![]() $G$
-set of left cosets
$G$
-set of left cosets
![]() $G/H_1 \cup G/H_2$
. The
$G/H_1 \cup G/H_2$
. The
![]() $\varphi$
-coalescence
$\varphi$
-coalescence
![]() $Z$
of
$Z$
of
![]() $ X$
with respect to the pair
$ X$
with respect to the pair
![]() $(H_1, H_2)$
is the quotient
$(H_1, H_2)$
is the quotient
![]() $G\times _A X$
by identifying
$G\times _A X$
by identifying
![]() $gtH_1$
and
$gtH_1$
and
![]() $gH_2$
for every
$gH_2$
for every
![]() $g\in G$
. Hence,
$g\in G$
. Hence,
![]() $Z$
is naturally isomorphic as a
$Z$
is naturally isomorphic as a
![]() $G$
-set to
$G$
-set to
![]() $G/H_1$
. Observe that the
$G/H_1$
. Observe that the
![]() $A$
-map
$A$
-map
![]() $X \to Z$
given by
$X \to Z$
given by
![]() $H_1\mapsto H_1$
and
$H_1\mapsto H_1$
and
![]() $\varphi (H_1)\mapsto tH_1$
is an injective
$\varphi (H_1)\mapsto tH_1$
is an injective
![]() $A$
-map.
$A$
-map.
Lemma 5.2.
Let
![]() $H$
be a subgroup of a group
$H$
be a subgroup of a group
![]() $A$
, let
$A$
, let
![]() $\varphi \;:\; H\to A$
be a monomorphism and let
$\varphi \;:\; H\to A$
be a monomorphism and let
![]() $G=A\ast _{\varphi }$
. Let
$G=A\ast _{\varphi }$
. Let
![]() $ X$
be an
$ X$
be an
![]() $A$
-set, let
$A$
-set, let
![]() $x,y\in X$
be in different
$x,y\in X$
be in different
![]() $A$
-orbits such that
$A$
-orbits such that
![]() $A_x=H$
,
$A_x=H$
,
![]() $A_y=\varphi (H)$
. If
$A_y=\varphi (H)$
. If
![]() $Z$
is the
$Z$
is the
![]() $\varphi$
-coalescence of
$\varphi$
-coalescence of
![]() $ X$
with respect to
$ X$
with respect to
![]() $(x,y)$
, and
$(x,y)$
, and
![]() $z=\rho (y)$
, then:
$z=\rho (y)$
, then:
-
1. the
 $G$
-stabilizer
$G$
-stabilizer
 $G_z$
equals
$G_z$
equals
 $\varphi (H)$
, and
$\varphi (H)$
, and
-
2. the
 $A$
-map
$A$
-map
 $\jmath \;:\; X \to Z$
defined by the commutative diagram
$\jmath \;:\; X \to Z$
defined by the commutative diagram

is injective.
Proof. The inclusion
![]() $\varphi (H) \subseteq G_z$
is a consequence of
$\varphi (H) \subseteq G_z$
is a consequence of
![]() $\rho$
being
$\rho$
being
![]() $G$
-equivariant,
$G$
-equivariant,
![]() $\varphi (H)=A_y$
and
$\varphi (H)=A_y$
and
![]() $\rho (y)=z$
. Conversely, let
$\rho (y)=z$
. Conversely, let
![]() $g\in G_z$
. Then
$g\in G_z$
. Then
![]() $g.y\sim y$
in
$g.y\sim y$
in
![]() $G\times _A X$
, and it follows that there is an integer
$G\times _A X$
, and it follows that there is an integer
![]() $n\geq 1$
and a sequence
$n\geq 1$
and a sequence
![]() $w_1, w_2,\ldots, w_n$
of elements of
$w_1, w_2,\ldots, w_n$
of elements of
![]() $G\times _A X$
such that
$G\times _A X$
such that
![]() $g.y=w_1$
,
$g.y=w_1$
,
![]() $w_n=y$
and
$w_n=y$
and
![]() $w_i$
and
$w_i$
and
![]() $w_{i+1}$
are the components of a basic relation (see the definition of coalescence). Since
$w_{i+1}$
are the components of a basic relation (see the definition of coalescence). Since
![]() $x$
and
$x$
and
![]() $y$
are in different
$y$
are in different
![]() $A$
-orbits in
$A$
-orbits in
![]() $X$
, they represent different
$X$
, they represent different
![]() $G$
-orbits in
$G$
-orbits in
![]() $G\times _A X$
, see the first item of Proposition 4.2. Hence, we have that
$G\times _A X$
, see the first item of Proposition 4.2. Hence, we have that
![]() $w_i=g_i.x$
if
$w_i=g_i.x$
if
![]() $i$
is even, and
$i$
is even, and
![]() $w_i=g_i.y$
if
$w_i=g_i.y$
if
![]() $i$
is odd, for some elements
$i$
is odd, for some elements
![]() $g_i$
of
$g_i$
of
![]() $G$
where
$G$
where
![]() $g_1=g$
and
$g_1=g$
and
![]() $g_n\in \phi (H)$
. Note that the integer
$g_n\in \phi (H)$
. Note that the integer
![]() $n$
is odd, and the chain of basic relations between the
$n$
is odd, and the chain of basic relations between the
![]() $w_i$
’s in
$w_i$
’s in
![]() $G\times _A X$
can be expressed as:
$G\times _A X$
can be expressed as:
By definition of basic relation,
![]() $tg_2^{-1}g_1\in \varphi (H)$
,
$tg_2^{-1}g_1\in \varphi (H)$
,
![]() $tg_2^{-1}g_3\in \varphi (H)$
,
$tg_2^{-1}g_3\in \varphi (H)$
,
![]() $tg_4^{-1}g_3\in \varphi (H)$
,
$tg_4^{-1}g_3\in \varphi (H)$
,
![]() $tg_4^{-1}g_5\in \varphi (H)$
, and so on until
$tg_4^{-1}g_5\in \varphi (H)$
, and so on until
![]() $tg_{n-1}^{-1}g_n\in \varphi (H)$
. Since
$tg_{n-1}^{-1}g_n\in \varphi (H)$
. Since
![]() $n$
is odd, we have that
$n$
is odd, we have that
which implies
![]() $g=g_1\in \varphi (H)$
. This shows that
$g=g_1\in \varphi (H)$
. This shows that
![]() $G_z=\varphi (H)$
$G_z=\varphi (H)$
Now we prove the second statement. By Lemma 4.2, the natural
![]() $A$
-map
$A$
-map
![]() $ X \to G\times _A X$
is injective. Observe that
$ X \to G\times _A X$
is injective. Observe that
![]() $Z$
is obtained as a quotient of
$Z$
is obtained as a quotient of
![]() $G\times _A X$
by the
$G\times _A X$
by the
![]() $G$
-equivariant equivalence relation generated by the basic relation
$G$
-equivariant equivalence relation generated by the basic relation
![]() $t.x \sim y$
. Hence to prove injectivity of
$t.x \sim y$
. Hence to prove injectivity of
![]() $X\to G\times _A X \to Z$
, it is enough to show that the restriction to
$X\to G\times _A X \to Z$
, it is enough to show that the restriction to
![]() $A.x \cup A.y$
is injective. Assume there are
$A.x \cup A.y$
is injective. Assume there are
![]() $a_1,a_2\in A$
such that
$a_1,a_2\in A$
such that
![]() $a_1.x$
and
$a_1.x$
and
![]() $a_2.x$
map to the same element in
$a_2.x$
map to the same element in
![]() $ Z$
. Then letting
$ Z$
. Then letting
![]() $a=a_2^{-1}a_1$
, both
$a=a_2^{-1}a_1$
, both
![]() $a.x$
and
$a.x$
and
![]() $x$
map to the same element in
$x$
map to the same element in
![]() $ Z$
. Hence,
$ Z$
. Hence,
![]() $a.x\sim x$
which implies that
$a.x\sim x$
which implies that
![]() $at^{-1}.y\sim t^{-1}.y$
. Therefore
$at^{-1}.y\sim t^{-1}.y$
. Therefore
![]() $(ta^{-1}t^{-1}).y\sim y$
and thus by the first statement,
$(ta^{-1}t^{-1}).y\sim y$
and thus by the first statement,
![]() $ta^{-1}t^{-1}\in \varphi (H)$
, and hence
$ta^{-1}t^{-1}\in \varphi (H)$
, and hence
![]() $a^{-1}\in t^{-1}\varphi (H)t=H$
. This results in
$a^{-1}\in t^{-1}\varphi (H)t=H$
. This results in
![]() $a\in H$
. Therefore,
$a\in H$
. Therefore,
![]() $a_2^{-1}a_1\in H$
and
$a_2^{-1}a_1\in H$
and
![]() $a_1.x=a_2.x$
. We have shown that the restriction
$a_1.x=a_2.x$
. We have shown that the restriction
![]() $A.x\to Z$
is injective. With a similar argument one can show that
$A.x\to Z$
is injective. With a similar argument one can show that
![]() $A.y \to Z$
is also injective.
$A.y \to Z$
is also injective.
Definition 5.3 (Coalescence in graphs). Let
![]() $H$
be a subgroup of a group
$H$
be a subgroup of a group
![]() $A$
, let
$A$
, let
![]() $\varphi \;:\; H\to A$
be a monomorphism, and let
$\varphi \;:\; H\to A$
be a monomorphism, and let
![]() $G=A\ast _{\varphi }$
. Let
$G=A\ast _{\varphi }$
. Let
![]() $\mathsf X$
be an
$\mathsf X$
be an
![]() $A$
-graph, let
$A$
-graph, let
![]() $x,y\in V(\mathsf X)$
such that
$x,y\in V(\mathsf X)$
such that
![]() $x\in X^H$
and
$x\in X^H$
and
![]() $y\in X^{\varphi (H)}$
. The
$y\in X^{\varphi (H)}$
. The
![]() $\varphi$
-Coalescence
$\varphi$
-Coalescence
![]() $\mathsf Z$
of
$\mathsf Z$
of
![]() $\mathsf X$
with respect to
$\mathsf X$
with respect to
![]() $(x,y)$
is the
$(x,y)$
is the
![]() $G$
-graph with vertex set the
$G$
-graph with vertex set the
![]() $\varphi$
-Coalescence of the
$\varphi$
-Coalescence of the
![]() $A$
-set
$A$
-set
![]() $V(\mathsf X)$
with respect to
$V(\mathsf X)$
with respect to
![]() $(x,y)$
, edge set
$(x,y)$
, edge set
![]() $G\times _A E(\mathsf X)$
, and attaching map
$G\times _A E(\mathsf X)$
, and attaching map
![]() $E(\mathsf Z) \to [V(Z)]^2$
defined as the composition
$E(\mathsf Z) \to [V(Z)]^2$
defined as the composition

where the horizontal middle arrows are induced by the attaching map
![]() $E(\mathsf X) \to [V(\mathsf X)]^2$
(see Lemma 4.2(3)) and the the bottom vertical map is induced by the quotient map
$E(\mathsf X) \to [V(\mathsf X)]^2$
(see Lemma 4.2(3)) and the the bottom vertical map is induced by the quotient map
![]() $G\times _AV(X) \to V(Z)$
. Let
$G\times _AV(X) \to V(Z)$
. Let
![]() $\rho \;:\; G\times _A \mathsf X \to \mathsf Z$
denote the induced
$\rho \;:\; G\times _A \mathsf X \to \mathsf Z$
denote the induced
![]() $G$
-morphism.
$G$
-morphism.
Remark 5.4 (Equivalent definition of coalescence). Equivalently, the
![]() $\varphi$
-coalescence
$\varphi$
-coalescence
![]() $\mathsf{Z}$
of the
$\mathsf{Z}$
of the
![]() $A$
-graph
$A$
-graph
![]() $\mathsf X$
with respect to
$\mathsf X$
with respect to
![]() $(x,y)$
is the quotient
$(x,y)$
is the quotient
![]() $\mathsf Z$
of the
$\mathsf Z$
of the
![]() $G$
-graph
$G$
-graph
![]() $G\times _A \mathsf X$
by the equivalence relation generated by
$G\times _A \mathsf X$
by the equivalence relation generated by
![]() $gt.x \sim g.y$
for all
$gt.x \sim g.y$
for all
![]() $g\in G$
.
$g\in G$
.
Proposition 5.5.
Let
![]() $H$
be a subgroup of a group
$H$
be a subgroup of a group
![]() $A$
, let
$A$
, let
![]() $\varphi \;:\; H\to A$
be a monomorphism and let
$\varphi \;:\; H\to A$
be a monomorphism and let
![]() $G=A\ast _{\varphi }$
. Let
$G=A\ast _{\varphi }$
. Let
![]() $\mathsf X$
be an
$\mathsf X$
be an
![]() $A$
-graph, let
$A$
-graph, let
![]() $x,y\in \mathsf X$
in different
$x,y\in \mathsf X$
in different
![]() $A$
-orbits such that
$A$
-orbits such that
![]() $A_x=H$
,
$A_x=H$
,
![]() $A_y=\varphi (H)$
. If
$A_y=\varphi (H)$
. If
![]() $\mathsf Z$
is the
$\mathsf Z$
is the
![]() $\varphi$
-coalescence of
$\varphi$
-coalescence of
![]() $\mathsf X$
with respect to
$\mathsf X$
with respect to
![]() $(x,y)$
, and
$(x,y)$
, and
![]() $z=\rho (y)$
, then the following properties hold:
$z=\rho (y)$
, then the following properties hold:
-
1.
 $G_z=\varphi (H)$
.
$G_z=\varphi (H)$
. -
2. The map
 $\mathsf{X}\hookrightarrow G\times _A \mathsf{X} \xrightarrow{} \mathsf{Z}$
is an
$\mathsf{X}\hookrightarrow G\times _A \mathsf{X} \xrightarrow{} \mathsf{Z}$
is an
 $A$
-equivariant embedding.
$A$
-equivariant embedding.
-
From here on, we consider
 $\mathsf X$
as a subgraph of
$\mathsf X$
as a subgraph of
 $\mathsf Z$
via this canonical embedding.
$\mathsf Z$
via this canonical embedding.
-
3. For every vertex
 $v$
(resp. edge
$v$
(resp. edge
 $e$
) of
$e$
) of
 $\mathsf Z$
, there is
$\mathsf Z$
, there is
 $g\in G$
such that
$g\in G$
such that
 $g.v$
is a vertex (resp. is an edge
$g.v$
is a vertex (resp. is an edge
 $g.e$
) of
$g.e$
) of
 $\mathsf X$
.
$\mathsf X$
. -
4. For every vertex
 $v$
of
$v$
of
 $\mathsf{X}$
which is not in the
$\mathsf{X}$
which is not in the
 $A$
-orbit of
$A$
-orbit of
 $x$
,
$x$
,
 $A_v = G_v$
where
$A_v = G_v$
where
 $G_v$
is the
$G_v$
is the
 $G$
-stabilizer of
$G$
-stabilizer of
 $v$
in
$v$
in
 $\mathsf Z$
.
$\mathsf Z$
. -
5. For every edge
 $e$
of
$e$
of
 $\mathsf X$
$\mathsf X$
 $A_e=G_e$
where
$A_e=G_e$
where
 $G_e$
is the
$G_e$
is the
 $G$
-stabilizer of
$G$
-stabilizer of
 $e$
in
$e$
in
 $\mathsf Z$
.
$\mathsf Z$
. -
6. If the complex
 $\mathsf X/ A$
has finitely many vertices (resp. edges), then
$\mathsf X/ A$
has finitely many vertices (resp. edges), then
 $\mathsf Z/ G$
has finitely many vertices (resp. edges).
$\mathsf Z/ G$
has finitely many vertices (resp. edges).
-
7. If
 $\mathsf{X}$
is connected, then
$\mathsf{X}$
is connected, then
 $\mathsf{Z}$
is connected.
$\mathsf{Z}$
is connected.
-
8. There is a
 $G$
-tree
$G$
-tree
 $T$
and a morphism
$T$
and a morphism
 $\xi \;:\; \mathsf Z \to T$
of
$\xi \;:\; \mathsf Z \to T$
of
 $G$
-graphs with the following properties: The
$G$
-graphs with the following properties: The
 $G$
-orbit of
$G$
-orbit of
 $\xi (z)$
and its complement in the set of vertices of
$\xi (z)$
and its complement in the set of vertices of
 $T$
make
$T$
make
 $T$
a bipartite
$T$
a bipartite
 $G$
-graph; the preimage
$G$
-graph; the preimage
 $\xi ^{-1}(\xi (z))$
is a single vertex; and if a vertex
$\xi ^{-1}(\xi (z))$
is a single vertex; and if a vertex
 $v$
of
$v$
of
 $T$
is not in the
$T$
is not in the
 $G$
-orbit of
$G$
-orbit of
 $\xi (z)$
, then the preimage of the star of
$\xi (z)$
, then the preimage of the star of
 $v$
is a subgraph of
$v$
is a subgraph of
 $\mathsf Z$
isomorphic to
$\mathsf Z$
isomorphic to
 $\mathsf X$
.
$\mathsf X$
.
The following argument is analogous to the proof of Proposition 4.5.
Proof. The first and second statements are direct consequences of Lemma 5.2 when considering
![]() $V(\mathsf X)$
and
$V(\mathsf X)$
and
![]() $E(\mathsf X)$
as
$E(\mathsf X)$
as
![]() $A$
-sets. Items three to six follow directly from the definition of
$A$
-sets. Items three to six follow directly from the definition of
![]() $\mathsf Z$
and Proposition 4.2.
$\mathsf Z$
and Proposition 4.2.
Suppose
![]() $\mathsf X$
is connected. By Proposition 4.2, the graph
$\mathsf X$
is connected. By Proposition 4.2, the graph
![]() $G\times _A \mathsf X$
is a disjoint union of copies of the connected subgraph
$G\times _A \mathsf X$
is a disjoint union of copies of the connected subgraph
![]() $\mathsf X$
, and hence any element in
$\mathsf X$
, and hence any element in
![]() $\mathsf Z$
belongs to a translate of
$\mathsf Z$
belongs to a translate of
![]() $\mathsf X$
by an element of
$\mathsf X$
by an element of
![]() $G$
. Therefore, to prove that
$G$
. Therefore, to prove that
![]() $\mathsf Z$
is connected, it is sufficient to show that for any
$\mathsf Z$
is connected, it is sufficient to show that for any
![]() $g\in G$
there is a path in
$g\in G$
there is a path in
![]() $\mathsf Z$
from
$\mathsf Z$
from
![]() $z$
to
$z$
to
![]() $g.z$
.
$g.z$
.
First observe that if there is a path from
![]() $z$
to
$z$
to
![]() $g.z$
, then there is a path from
$g.z$
, then there is a path from
![]() $z$
to
$z$
to
![]() $gt.z$
. Indeed, there is a path from
$gt.z$
. Indeed, there is a path from
![]() $x$
to
$x$
to
![]() $y$
in the connected subgraph
$y$
in the connected subgraph
![]() $\mathsf X$
of
$\mathsf X$
of
![]() $G\times _A \mathsf X$
, and hence there is a path from
$G\times _A \mathsf X$
, and hence there is a path from
![]() $z=\rho (t.x)$
to
$z=\rho (t.x)$
to
![]() $t.z=\rho (t.y)$
in
$t.z=\rho (t.y)$
in
![]() $\mathsf Z$
. Therefore, there is a path from
$\mathsf Z$
. Therefore, there is a path from
![]() $g.z$
to
$g.z$
to
![]() $gt.z$
in
$gt.z$
in
![]() $\mathsf Z$
, and in particular a path from
$\mathsf Z$
, and in particular a path from
![]() $z$
to
$z$
to
![]() $gt.z$
.
$gt.z$
.
Now observe that if there is a path from
![]() $z$
to
$z$
to
![]() $g.z$
, then there is a path from
$g.z$
, then there is a path from
![]() $z$
to
$z$
to
![]() $ga.z$
for any
$ga.z$
for any
![]() $a\in A$
. Indeed, there is a path from
$a\in A$
. Indeed, there is a path from
![]() $z$
to
$z$
to
![]() $a.z$
in the connected
$a.z$
in the connected
![]() $A$
-subgraph
$A$
-subgraph
![]() $\mathsf X$
of
$\mathsf X$
of
![]() $\mathsf Z$
. Hence, there is a path from
$\mathsf Z$
. Hence, there is a path from
![]() $g.z$
to
$g.z$
to
![]() $ga.z$
in
$ga.z$
in
![]() $\mathsf Z$
, and in particular a path from
$\mathsf Z$
, and in particular a path from
![]() $z$
to
$z$
to
![]() $ga.z$
.
$ga.z$
.
To conclude, any
![]() $g\in G$
is a product of the form
$g\in G$
is a product of the form
![]() $g=a_1t^{\theta _1}a_2t^{\theta _2}\ldots a_nt^{\theta _n}a_{n+1}$
with
$g=a_1t^{\theta _1}a_2t^{\theta _2}\ldots a_nt^{\theta _n}a_{n+1}$
with
![]() $a_i\in A$
and
$a_i\in A$
and
![]() $\theta _i=\pm 1$
. Therefore, an induction argument using the two previous statements shows that there is a path from
$\theta _i=\pm 1$
. Therefore, an induction argument using the two previous statements shows that there is a path from
![]() $z$
to
$z$
to
![]() $g.z$
in
$g.z$
in
![]() $\mathsf Z$
for every
$\mathsf Z$
for every
![]() $g\in G$
.
$g\in G$
.
Now we prove the eighth statement. Consider the barycentric subdivision
![]() $T$
of the Bass–Serre tree of the splitting
$T$
of the Bass–Serre tree of the splitting
![]() $G\ast _{\varphi }$
. Specifically,
$G\ast _{\varphi }$
. Specifically,
![]() $T$
is the tree with vertex set
$T$
is the tree with vertex set
edge set
Note that all the edges of
![]() $T$
are
$T$
are
![]() $G$
-translates of the following two edges attached at the vertex
$G$
-translates of the following two edges attached at the vertex
![]() $tH$
,
$tH$
,

Suppose that the
![]() $A$
-set
$A$
-set
![]() $V(\mathsf X)=\left (\bigsqcup _{i\in I}A/A_i\right ) \sqcup A/H \sqcup A/\varphi (H)$
. Then
$V(\mathsf X)=\left (\bigsqcup _{i\in I}A/A_i\right ) \sqcup A/H \sqcup A/\varphi (H)$
. Then
 \begin{equation*}V(G\times _A \mathsf X)=\left(\bigsqcup _{i\in I }G/A_i\right)\sqcup G/H\sqcup G/\varphi (H).\end{equation*}
\begin{equation*}V(G\times _A \mathsf X)=\left(\bigsqcup _{i\in I }G/A_i\right)\sqcup G/H\sqcup G/\varphi (H).\end{equation*}
Since
![]() $T$
is a simplicial graph, there is an induced
$T$
is a simplicial graph, there is an induced
![]() $G$
-equivariant morphism of graphs
$G$
-equivariant morphism of graphs
defined on vertices by:
Note that any edge in
![]() $G\times _A \mathsf X$
of the form
$G\times _A \mathsf X$
of the form
![]() $\{gA_i,gaA_j\}$
for
$\{gA_i,gaA_j\}$
for
![]() $g\in G$
and
$g\in G$
and
![]() $a\in A$
is collapsed to the vertex
$a\in A$
is collapsed to the vertex
![]() $gA$
in
$gA$
in
![]() $T$
; and edges of the form
$T$
; and edges of the form
![]() $\{gA_i, gH\}$
and
$\{gA_i, gH\}$
and
![]() $\{gA_i, gtH \}$
are mapped to the edges
$\{gA_i, gtH \}$
are mapped to the edges
![]() $\{gA, gH\}$
and
$\{gA, gH\}$
and
![]() $\{gA, g\varphi (H)\}$
of
$\{gA, g\varphi (H)\}$
of
![]() $T$
, respectively. This map induces a
$T$
, respectively. This map induces a
![]() $G$
-equivariant morphism of graphs
$G$
-equivariant morphism of graphs
![]() $\xi \;:\; \mathsf Z\to T$
such that the following diagram commutes,
$\xi \;:\; \mathsf Z\to T$
such that the following diagram commutes,

Indeed this diagram commutes since
![]() $\psi$
is
$\psi$
is
![]() $G$
-equivariant and
$G$
-equivariant and
![]() $\psi (tH)=\psi (\varphi (H))$
.
$\psi (tH)=\psi (\varphi (H))$
.
Observe that
![]() $\xi (z)=\psi (tH)$
and
$\xi (z)=\psi (tH)$
and
![]() $\psi ^{-1}(tH)=\{tH,\varphi (H)\}$
, then
$\psi ^{-1}(tH)=\{tH,\varphi (H)\}$
, then
![]() $\rho (tH)=\rho (\varphi (H))$
implies that
$\rho (tH)=\rho (\varphi (H))$
implies that
![]() $\xi ^{-1}(\xi (z))=\{z\}$
.
$\xi ^{-1}(\xi (z))=\{z\}$
.
By definition of
![]() $T$
, if a vertex
$T$
, if a vertex
![]() $v$
is not in the
$v$
is not in the
![]() $G$
-orbit of
$G$
-orbit of
![]() $\xi (z)=tH$
, then
$\xi (z)=tH$
, then
![]() $v\in G/A$
. Hence, the partition
$v\in G/A$
. Hence, the partition
![]() $V(T)=G/A\sqcup G/H$
‘ makes
$V(T)=G/A\sqcup G/H$
‘ makes
![]() $T$
a bipartite
$T$
a bipartite
![]() $G$
-graph. Any edge of
$G$
-graph. Any edge of
![]() $\mathsf{star}_T(A)$
is of the form
$\mathsf{star}_T(A)$
is of the form
![]() $\{A,atH\}$
for some
$\{A,atH\}$
for some
![]() $a\in A$
. Hence,
$a\in A$
. Hence,
![]() $\xi ^{-1}(\mathsf{star}_T(A))=\rho (\psi ^{-1}(\mathsf{star}_T(A))) = \rho ( \mathsf{X})$
and then the definition of
$\xi ^{-1}(\mathsf{star}_T(A))=\rho (\psi ^{-1}(\mathsf{star}_T(A))) = \rho ( \mathsf{X})$
and then the definition of
![]() $Z$
implies that
$Z$
implies that
![]() $\rho ( \mathsf{X})$
is isomorphic
$\rho ( \mathsf{X})$
is isomorphic
![]() $\mathsf{X}$
.
$\mathsf{X}$
.
Proof of Theorem 3.2. The argument is the same as the one used to prove Theorem 3.1, the only difference is the use of Proposition 5.5 instead of Proposition 4.5.
6. Dehn functions and coarse isoperimetric functions
In this section, we recall the definition of coarse isoperimetric function of a graph and recall how one can recover the relative Dehn function of a pair via Cayley–Abels graphs; see Theorem 6.4. In the second part of the section, we discuss a technical result that provides bounds for coarse isoperimetric functions of graphs based on maps into trees; see Proposition 6.6. These results are used to obtain bounds on the relative Dehn function of fundamental groups of graph of groups based on the relative Dehn functions of the vertex groups; see Corollary 1.6.
6.1. Coarse isoperimetric functions
A singular combinatorial map
![]() $X\to Y$
between one-dimensional CW-complexes is a continuous map such that the restriction to each open one-dimensional cell of
$X\to Y$
between one-dimensional CW-complexes is a continuous map such that the restriction to each open one-dimensional cell of
![]() $X$
is either a homeomorphism onto an open cell of
$X$
is either a homeomorphism onto an open cell of
![]() $Y$
or its image is contained in the 0-skeleton of
$Y$
or its image is contained in the 0-skeleton of
![]() $Y$
. A singular combinatorial loop
$Y$
. A singular combinatorial loop
![]() $c\;:\; I\to X$
is a singular combinatorial map such that its domain is a CW-complex homeomorphic to a closed interval. The length
$c\;:\; I\to X$
is a singular combinatorial map such that its domain is a CW-complex homeomorphic to a closed interval. The length
![]() $\mathsf{Len}(c)$
of
$\mathsf{Len}(c)$
of
![]() $c$
is defined as the number of open 1-cells of
$c$
is defined as the number of open 1-cells of
![]() $I$
that map homeomorphically to open cells of
$I$
that map homeomorphically to open cells of
![]() $X$
.
$X$
.
Let
![]() $\Gamma$
be a connected graph, regard it as a CW-complex, and consider the path-metric on
$\Gamma$
be a connected graph, regard it as a CW-complex, and consider the path-metric on
![]() $\Gamma$
obtained by regarding each edge as a segment of unit length. Let
$\Gamma$
obtained by regarding each edge as a segment of unit length. Let
![]() $k\gt 0$
. An
$k\gt 0$
. An
![]() $k$
-filling of a singular combinatorial loop
$k$
-filling of a singular combinatorial loop
![]() $c\;:\; I \to \Gamma$
is a pair
$c\;:\; I \to \Gamma$
is a pair
![]() $(P,\Phi )$
consisting of a triangulation
$(P,\Phi )$
consisting of a triangulation
![]() $P$
of the
$P$
of the
![]() $2$
-disc
$2$
-disc
![]() $D^2$
and a singular combinatorial map
$D^2$
and a singular combinatorial map
![]() $\Phi \;:\; P^{(1)}\to \Gamma$
such that
$\Phi \;:\; P^{(1)}\to \Gamma$
such that
![]() $\Phi |_{\partial D}$
equals the closed path
$\Phi |_{\partial D}$
equals the closed path
![]() $c$
(after identifying the endpoints of the domain of
$c$
(after identifying the endpoints of the domain of
![]() $c$
) and the image under
$c$
) and the image under
![]() $\Phi$
of the boundary of each 2-cell of
$\Phi$
of the boundary of each 2-cell of
![]() $P$
is a set of diameter at most
$P$
is a set of diameter at most
![]() $k$
in
$k$
in
![]() $\Gamma$
. Define
$\Gamma$
. Define
![]() $|(P,\Phi )|$
to be the number of faces of
$|(P,\Phi )|$
to be the number of faces of
![]() $P$
and
$P$
and
The
![]() $k$
-coarse isoperimetric function
$k$
-coarse isoperimetric function
![]() $f_k^\Gamma \;:\; \mathbb{N}\to \mathbb{N}$
of
$f_k^\Gamma \;:\; \mathbb{N}\to \mathbb{N}$
of
![]() $\Gamma$
is then defined to be
$\Gamma$
is then defined to be
We say that
![]() $f^\Gamma _k$
is well defined if it takes only finite values. The graph
$f^\Gamma _k$
is well defined if it takes only finite values. The graph
![]() $\Gamma$
is
$\Gamma$
is
![]() $k$
-fillable if
$k$
-fillable if
![]() $f_k^\Gamma$
is well defined, and
$f_k^\Gamma$
is well defined, and
![]() $\Gamma$
is fillable if it is
$\Gamma$
is fillable if it is
![]() $k$
-fillable for some integer
$k$
-fillable for some integer
![]() $k$
. Note that if
$k$
. Note that if
![]() $f_k^\Gamma$
is well defined then
$f_k^\Gamma$
is well defined then
![]() $f_\ell ^\Gamma$
is well defined for all
$f_\ell ^\Gamma$
is well defined for all
![]() $\ell \geq k$
.
$\ell \geq k$
.
For two functions
![]() $f,g\;:\; \mathbb{N}\to \mathbb{N}$
, define
$f,g\;:\; \mathbb{N}\to \mathbb{N}$
, define
![]() $f\preceq g$
if there exist constants
$f\preceq g$
if there exist constants
![]() $C,K,L\in \mathbb{N}$
such that
$C,K,L\in \mathbb{N}$
such that
We say that
![]() $f$
is asymptotically equivalent to
$f$
is asymptotically equivalent to
![]() $g$
if
$g$
if
![]() $f \asymp g$
if
$f \asymp g$
if
![]() $f\preceq g$
and
$f\preceq g$
and
![]() $g\preceq f$
.
$g\preceq f$
.
Proposition 6.1. [Reference Bridson and Haefliger4, Proposition III.H.2.2] If
![]() $\Gamma$
and
$\Gamma$
and
![]() $\Gamma '$
are quasi-isometric connected graphs such that
$\Gamma '$
are quasi-isometric connected graphs such that
![]() $\Gamma$
is fillable, then
$\Gamma$
is fillable, then
![]() $\Gamma '$
is fillable and
$\Gamma '$
is fillable and
![]() $f_k^{\Gamma }\asymp f_k^{\Gamma '}$
for all sufficiently large integers
$f_k^{\Gamma }\asymp f_k^{\Gamma '}$
for all sufficiently large integers
![]() $k$
.
$k$
.
We conclude the subsection recalling two results in order to deduce Corollary 6.4 which shows that the relative Dehn function of a finitely presented pair is equivalent to coarse isoperimetric fuctions of Cayley–Abels graphs.
The following theorem is a re-statement of a result of Osin; see [Reference Hughes, Martínez-Pedroza and Saldana12, Prop. 4.8].
Theorem 6.2. [Reference Osin18, Thm. 2.53] Let
![]() $G$
be a group and let
$G$
be a group and let
![]() $\mathcal{H}$
be a collection of subgroups. If
$\mathcal{H}$
be a collection of subgroups. If
![]() $\Delta _{G,\mathcal{H}}$
is well defined, then
$\Delta _{G,\mathcal{H}}$
is well defined, then
![]() $\hat \Gamma (G,\mathcal{H})$
is fillable and
$\hat \Gamma (G,\mathcal{H})$
is fillable and
![]() $\Delta _{G,\mathcal{H}} \asymp f^{\hat \Gamma (G,\mathcal{H})}_k$
for all sufficiently large integers
$\Delta _{G,\mathcal{H}} \asymp f^{\hat \Gamma (G,\mathcal{H})}_k$
for all sufficiently large integers
![]() $k$
.
$k$
.
Theorem 6.3. [Reference Hughes, Martínez-Pedroza and Saldana12, Theorem E] Let
![]() $(G,\mathcal{H})$
be a finitely generated pair. If
$(G,\mathcal{H})$
be a finitely generated pair. If
![]() $\hat \Gamma (G,\mathcal{H})$
is fine and fillable, then
$\hat \Gamma (G,\mathcal{H})$
is fine and fillable, then
![]() $(G, \mathcal{H})$
is finitely presented and
$(G, \mathcal{H})$
is finitely presented and
![]() $\Delta _{G,\mathcal{H}}$
is well defined.
$\Delta _{G,\mathcal{H}}$
is well defined.
As previously observed, the coned-off Cayley graphs of a finitely generated pair
![]() $(G,\mathcal{H})$
are Cayley–Abels graphs of the pair. Theorem 2.12 states that all Cayley–Abels graphs of a finitely generated pair are quasi-isometric, and if one of them is fine then all of them are fine. Moreover, fillable and the class of coarse isoperimetric functions are quasi-isometry invariants of graphs by Proposition 6.2. Putting these results together with the two results above, and Theorem 2.11, one obtains the following corollary.
$(G,\mathcal{H})$
are Cayley–Abels graphs of the pair. Theorem 2.12 states that all Cayley–Abels graphs of a finitely generated pair are quasi-isometric, and if one of them is fine then all of them are fine. Moreover, fillable and the class of coarse isoperimetric functions are quasi-isometry invariants of graphs by Proposition 6.2. Putting these results together with the two results above, and Theorem 2.11, one obtains the following corollary.
Corollary 6.4.
Let
![]() $\Gamma$
be a Cayley–Abels graph of finitely generated proper pair
$\Gamma$
be a Cayley–Abels graph of finitely generated proper pair
![]() $(G,\mathcal{H})$
.
$(G,\mathcal{H})$
.
-
1. If
 $\Delta _{G,\mathcal{H}}$
is well defined, then
$\Delta _{G,\mathcal{H}}$
is well defined, then
 $\Gamma$
is fine and fillable, and
$\Gamma$
is fine and fillable, and
 $\Delta _{G,\mathcal{H}} \asymp f^{\Gamma }_k$
for all sufficiently large integers
$\Delta _{G,\mathcal{H}} \asymp f^{\Gamma }_k$
for all sufficiently large integers
 $k$
.
$k$
. -
2. If
 $\Gamma$
is fine and fillable, then
$\Gamma$
is fine and fillable, then
 $(G, \mathcal{H})$
is finitely presented and
$(G, \mathcal{H})$
is finitely presented and
 $\Delta _{G,\mathcal{H}}$
is well defined.
$\Delta _{G,\mathcal{H}}$
is well defined.
6.2. Relative Dehn functions and splittings
Let
![]() $g\;:\; \mathbb{N} \to \mathbb{N}$
be a function. Then
$g\;:\; \mathbb{N} \to \mathbb{N}$
be a function. Then
![]() $g$
is superadditive if
$g$
is superadditive if
![]() $g(m)+g(n)\leq g(m+n)$
. If
$g(m)+g(n)\leq g(m+n)$
. If
![]() $g(0)=0$
then the super-additive closure
$g(0)=0$
then the super-additive closure
![]() $\overline{g}\;:\; \mathbb{N} \to \mathbb{N}$
of
$\overline{g}\;:\; \mathbb{N} \to \mathbb{N}$
of
![]() $g$
is the function:
$g$
is the function:
 \begin{equation*} \overline {g}(n) = \max \left \{ \sum _{i=1}^k g(n_i) \mid k\in \mathbb {N},\ n_i\in \mathbb {N},\ \sum _{i=1}^kn_i=n \right \},\end{equation*}
\begin{equation*} \overline {g}(n) = \max \left \{ \sum _{i=1}^k g(n_i) \mid k\in \mathbb {N},\ n_i\in \mathbb {N},\ \sum _{i=1}^kn_i=n \right \},\end{equation*}
and it is an observation that
![]() $\bar g$
is the least super-additive function such that
$\bar g$
is the least super-additive function such that
![]() $g(n)\leq \overline{g}(n)$
for all
$g(n)\leq \overline{g}(n)$
for all
![]() $n$
. Note that the requirement
$n$
. Note that the requirement
![]() $g(0)=0$
is necessary in order for
$g(0)=0$
is necessary in order for
![]() $\bar g$
to be well defined. An outstanding open question raised by Mark Sapir is whether the Dehn function of any finite presentation is asymptotically equivalent to a superadditive function [Reference Guba and Sapir11].
$\bar g$
to be well defined. An outstanding open question raised by Mark Sapir is whether the Dehn function of any finite presentation is asymptotically equivalent to a superadditive function [Reference Guba and Sapir11].
Proposition 6.5.
Let
![]() $r\;:\; \Gamma \to \Delta$
be a retraction of graphs. If
$r\;:\; \Gamma \to \Delta$
be a retraction of graphs. If
![]() $\Gamma$
is
$\Gamma$
is
![]() $k$
-fillable, then
$k$
-fillable, then
![]() $\Delta$
is
$\Delta$
is
![]() $k$
-fillable and
$k$
-fillable and
![]() $f_k^\Delta (n)\leq f_k^\Gamma (n)$
.
$f_k^\Delta (n)\leq f_k^\Gamma (n)$
.
Proof. Let
![]() $c\;:\; I\to \Delta$
is a singular combinatorial loop. If
$c\;:\; I\to \Delta$
is a singular combinatorial loop. If
![]() $(P,\Phi )$
is a
$(P,\Phi )$
is a
![]() $k$
-filling of
$k$
-filling of
![]() $c$
in
$c$
in
![]() $\Gamma$
then it is an observation that
$\Gamma$
then it is an observation that
![]() $(P,r\circ \Phi )$
is a
$(P,r\circ \Phi )$
is a
![]() $k$
-filling of
$k$
-filling of
![]() $c$
in
$c$
in
![]() $\Delta$
. Therefore,
$\Delta$
. Therefore,
![]() ${\mathsf{area}}_k^\Delta (c)\leq{\mathsf{area}}_k^\Gamma (c)$
and the result follows.
${\mathsf{area}}_k^\Delta (c)\leq{\mathsf{area}}_k^\Gamma (c)$
and the result follows.
The following proposition is the main technical result of the section.
Proposition 6.6.
Let
![]() $\xi \;:\; \Gamma \to T$
be a morphism of graphs where
$\xi \;:\; \Gamma \to T$
be a morphism of graphs where
![]() $T$
is a bipartite tree, say
$T$
is a bipartite tree, say
![]() $V(T)=K \cup L$
. Suppose
$V(T)=K \cup L$
. Suppose
![]() $\xi ^{-1}(v)$
is a single vertex for every
$\xi ^{-1}(v)$
is a single vertex for every
![]() $v\in L$
, and
$v\in L$
, and
![]() $\xi ^{-1}(\mathsf{star}(v))$
is a connected subgraph for every
$\xi ^{-1}(\mathsf{star}(v))$
is a connected subgraph for every
![]() $v\in K$
. Let
$v\in K$
. Let
![]() $\Omega = \{ \xi ^{-1}(\mathsf{star}(v)) \mid v\in K \}$
.
$\Omega = \{ \xi ^{-1}(\mathsf{star}(v)) \mid v\in K \}$
.
If there is
![]() $k\gt 0$
such that each
$k\gt 0$
such that each
![]() $\Delta \in \Omega$
is a
$\Delta \in \Omega$
is a
![]() $k$
-fillable graph and
$k$
-fillable graph and
then
![]() $\Gamma$
is
$\Gamma$
is
![]() $k$
-fillable and
$k$
-fillable and
where
![]() $\overline{g}$
denotes the super-additive closure of the function
$\overline{g}$
denotes the super-additive closure of the function
![]() $g\;:\; \mathbb{N}\to \mathbb{N}$
.
$g\;:\; \mathbb{N}\to \mathbb{N}$
.
Proof. It is an observation that if
![]() $c_1$
and
$c_1$
and
![]() $c_2$
are singular combinatorial loops in
$c_2$
are singular combinatorial loops in
![]() $\Gamma$
with the same initial point, and both admit
$\Gamma$
with the same initial point, and both admit
![]() $k$
-fillings, then the concatenated loop
$k$
-fillings, then the concatenated loop
![]() $c_1\cdot c_2$
admits a
$c_1\cdot c_2$
admits a
![]() $k$
-filling and
$k$
-filling and
To prove that
![]() $f_k^\Gamma (n)\leq \overline{g}(n)$
, we prove that if
$f_k^\Gamma (n)\leq \overline{g}(n)$
, we prove that if
![]() $c\;:\; I \to \Gamma$
is a singular combinatorial loop in
$c\;:\; I \to \Gamma$
is a singular combinatorial loop in
![]() $\Gamma$
then
$\Gamma$
then
![]() ${\mathsf{area}}^\Gamma _k(c)\leq \overline{g}(\mathsf{Len}(c))$
.
${\mathsf{area}}^\Gamma _k(c)\leq \overline{g}(\mathsf{Len}(c))$
.
Let
![]() $c\;:\; I \to \Gamma$
be a singular combinatorial loop in
$c\;:\; I \to \Gamma$
be a singular combinatorial loop in
![]() $\Gamma$
. Consider the loop
$\Gamma$
. Consider the loop
![]() $\xi \circ c$
in the tree
$\xi \circ c$
in the tree
![]() $T$
. The image of
$T$
. The image of
![]() $\xi \circ c$
is a finite subtree
$\xi \circ c$
is a finite subtree
![]() $T_c$
of
$T_c$
of
![]() $T$
. Let
$T$
. Let
![]() $\#T_c\cap K$
denote the number of vertices of
$\#T_c\cap K$
denote the number of vertices of
![]() $T_c$
that belong to
$T_c$
that belong to
![]() $K$
. To the loop
$K$
. To the loop
![]() $c$
assign the complexity
$c$
assign the complexity
![]() $|c|=(\#T_c\cap K, \mathsf{Len}(c)) \in \mathbb{N}\times \mathbb{N}$
. Consider the lexicographical order on
$|c|=(\#T_c\cap K, \mathsf{Len}(c)) \in \mathbb{N}\times \mathbb{N}$
. Consider the lexicographical order on
![]() $\mathbb{N}\times \mathbb{N}$
, and recall that this is well-ordered set. We prove by induction on
$\mathbb{N}\times \mathbb{N}$
, and recall that this is well-ordered set. We prove by induction on
![]() $(\#T_c\cap K, \mathsf{Len}(c))$
that
$(\#T_c\cap K, \mathsf{Len}(c))$
that
![]() ${\mathsf{area}}^\Gamma _k(c)\leq \overline{g}(\mathsf{Len}(c))$
.
${\mathsf{area}}^\Gamma _k(c)\leq \overline{g}(\mathsf{Len}(c))$
.
Base case
![]() $|c|=(0,m)$
. Suppose that
$|c|=(0,m)$
. Suppose that
![]() $T_c$
does not contain vertices in
$T_c$
does not contain vertices in
![]() $K$
. In this case, the bipartite assumption on
$K$
. In this case, the bipartite assumption on
![]() $T$
implies that
$T$
implies that
![]() $T_c$
consists of a single vertex
$T_c$
consists of a single vertex
![]() $v$
in
$v$
in
![]() $L$
. Since
$L$
. Since
![]() $\xi ^{-1}(v)$
is a single vertex of
$\xi ^{-1}(v)$
is a single vertex of
![]() $\Gamma$
, it follows that
$\Gamma$
, it follows that
![]() $c$
is constant path and hence
$c$
is constant path and hence
![]() $\mathsf{Len}(c)=0$
and
$\mathsf{Len}(c)=0$
and
![]() ${\mathsf{area}}^\Gamma _k(c)=0\leq \overline{g}(0)$
.
${\mathsf{area}}^\Gamma _k(c)=0\leq \overline{g}(0)$
.
Base case
![]() $|c|=(1,m)$
. Suppose that the vertex set of
$|c|=(1,m)$
. Suppose that the vertex set of
![]() $T_c$
contains a single vertex in
$T_c$
contains a single vertex in
![]() $K$
, say
$K$
, say
![]() $v$
. Then the bipartite assumption on
$v$
. Then the bipartite assumption on
![]() $T$
implies that
$T$
implies that
![]() $T_c$
is a subgraph of
$T_c$
is a subgraph of
![]() $\mathsf{star}(v)$
and hence the image of
$\mathsf{star}(v)$
and hence the image of
![]() $c$
is contained in the subgraph
$c$
is contained in the subgraph
![]() $\Delta =\xi ^{-1}(\mathsf{star}(v))$
. By assumption,
$\Delta =\xi ^{-1}(\mathsf{star}(v))$
. By assumption,
![]() $\Delta$
is
$\Delta$
is
![]() $k$
-fillable, and hence there is
$k$
-fillable, and hence there is
![]() $k$
-filling of
$k$
-filling of
![]() $c$
in
$c$
in
![]() $\Delta$
which is trivially also a
$\Delta$
which is trivially also a
![]() $k$
-filling in
$k$
-filling in
![]() $\Gamma$
. Hence,
$\Gamma$
. Hence,
General case
![]() $|c|=(n, m)$
with
$|c|=(n, m)$
with
![]() $n\geq 2$
. For the inductive step, suppose that
$n\geq 2$
. For the inductive step, suppose that
![]() $T_c\cap K$
has at least two vertices in
$T_c\cap K$
has at least two vertices in
![]() $K$
. Without loss of generality, we can identify the domain
$K$
. Without loss of generality, we can identify the domain
![]() $I$
of
$I$
of
![]() $c$
with the closed interval
$c$
with the closed interval
![]() $[0,1]$
(with some CW-structure). Since
$[0,1]$
(with some CW-structure). Since
![]() $T_c$
is connected, the bipartite assumption on
$T_c$
is connected, the bipartite assumption on
![]() $T$
, implies that
$T$
, implies that
![]() $T_c$
contains a vertex
$T_c$
contains a vertex
![]() $v\in L$
such that
$v\in L$
such that
![]() $v$
is not a leaf of
$v$
is not a leaf of
![]() $T_c$
, in particular,
$T_c$
, in particular,
![]() $T_c-\{v\}$
has at least two connected components. Then
$T_c-\{v\}$
has at least two connected components. Then
![]() $(\xi \circ c)^{-1}(T_c-\{v\})$
is a disconnected open subset of
$(\xi \circ c)^{-1}(T_c-\{v\})$
is a disconnected open subset of
![]() $[0,1]$
. Let
$[0,1]$
. Let
![]() $J_1$
be the closure of a connected component of
$J_1$
be the closure of a connected component of
![]() $(\xi \circ c)^{-1}(T_c-\{v\})$
. By changing the initial point of the loop
$(\xi \circ c)^{-1}(T_c-\{v\})$
. By changing the initial point of the loop
![]() $c\;:\; I \to \Gamma$
, we can assume that
$c\;:\; I \to \Gamma$
, we can assume that
![]() $J_1=[0,\alpha ]$
for some
$J_1=[0,\alpha ]$
for some
![]() $\alpha \lt 1$
. Let
$\alpha \lt 1$
. Let
![]() $J_2=[\alpha,1]$
, and let
$J_2=[\alpha,1]$
, and let
![]() $c_i$
be the restriction of
$c_i$
be the restriction of
![]() $c$
to the interval
$c$
to the interval
![]() $J_i$
. Then
$J_i$
. Then
![]() $c_i$
is singular combinatorial loop, and
$c_i$
is singular combinatorial loop, and
![]() $c$
is the concatenation
$c$
is the concatenation
![]() $c_1\cdot c_2$
. Since
$c_1\cdot c_2$
. Since
![]() $T_c-\{v\}$
is disconnected, it follows that
$T_c-\{v\}$
is disconnected, it follows that
![]() $0\lt \mathsf{Len}(c_i)\lt \mathsf{Len}(c)$
. Since
$0\lt \mathsf{Len}(c_i)\lt \mathsf{Len}(c)$
. Since
![]() $\#T_{c_i}\cap K \leq \#T_c\cap K$
, it follows that
$\#T_{c_i}\cap K \leq \#T_c\cap K$
, it follows that
![]() $|c_i|\lt |c|$
. Hence by induction
$|c_i|\lt |c|$
. Hence by induction
 \begin{align*} \begin{split}{\mathsf{area}}^\Gamma _k(c) & \leq{\mathsf{area}}^\Gamma _k(c_1) +{\mathsf{area}}^\Gamma _k(c_2) \\ & \leq \overline{g}(\mathsf{Len}(c_1))+ \overline{g}(\mathsf{Len}(c_2)) \\ & \leq \overline{g}(\mathsf{Len}(c_1) + \mathsf{Len}(c_2)) = \overline{g}(\mathsf{Len}(c)) \end{split} \end{align*}
\begin{align*} \begin{split}{\mathsf{area}}^\Gamma _k(c) & \leq{\mathsf{area}}^\Gamma _k(c_1) +{\mathsf{area}}^\Gamma _k(c_2) \\ & \leq \overline{g}(\mathsf{Len}(c_1))+ \overline{g}(\mathsf{Len}(c_2)) \\ & \leq \overline{g}(\mathsf{Len}(c_1) + \mathsf{Len}(c_2)) = \overline{g}(\mathsf{Len}(c)) \end{split} \end{align*}
where the first inequality follows from the observation in the first paragraph of this proof, the second inequality uses the induction hypothesis, and the third one uses that
![]() $\overline{g}$
is superadditive.
$\overline{g}$
is superadditive.
6.3. Proof of Theorem 1.6
Proof. The proofs of the first two statements are analogous, and the argument goes back to the method of proof of the corresponding theorems in the introduction. The third statement is a consequence of the second one; see the proof of Corollary 1.4(2).
We prove the first statement and leave the proof of the second statement to the reader. We remark that the argument essentially reproves Theorem 1.2(2).
Let
![]() $\Gamma _i$
be a Cayley–Abels graph of
$\Gamma _i$
be a Cayley–Abels graph of
![]() $(G_i, \mathcal{H}_i \cup \{K_i\})$
for
$(G_i, \mathcal{H}_i \cup \{K_i\})$
for
![]() $i=1,2$
. Then
$i=1,2$
. Then
![]() $\Gamma _i$
has a vertex
$\Gamma _i$
has a vertex
![]() $x_i$
with
$x_i$
with
![]() $G_i$
-stabilizer
$G_i$
-stabilizer
![]() $K_i$
. Let
$K_i$
. Let
![]() $\Gamma$
be the
$\Gamma$
be the
![]() $C$
-pushout of
$C$
-pushout of
![]() $G\times _{G_1} \Gamma _1$
and
$G\times _{G_1} \Gamma _1$
and
![]() $G\times _{G_2} \Gamma _2$
with respect to
$G\times _{G_2} \Gamma _2$
with respect to
![]() $(x_1,x_2)$
. Theorem 3.1 implies that
$(x_1,x_2)$
. Theorem 3.1 implies that
![]() $\Gamma$
is a Cayley–Abels graph of
$\Gamma$
is a Cayley–Abels graph of
![]() $(G_1\ast _C G_2, \mathcal{H} \cup \{\langle K_1,K_2 \rangle \})$
. By Proposition 4.5(8), there is a morphism of graphs
$(G_1\ast _C G_2, \mathcal{H} \cup \{\langle K_1,K_2 \rangle \})$
. By Proposition 4.5(8), there is a morphism of graphs
![]() $\xi \;:\; \Gamma \to T$
that satisfies the hypothesis of Proposition 6.6, namely,
$\xi \;:\; \Gamma \to T$
that satisfies the hypothesis of Proposition 6.6, namely,
![]() $T$
is a bipartite tree with
$T$
is a bipartite tree with
![]() $V(T)=K\cup L$
such that
$V(T)=K\cup L$
such that
![]() $\xi ^{-1}(v)$
is a single vertex for each
$\xi ^{-1}(v)$
is a single vertex for each
![]() $v\in L$
, and
$v\in L$
, and
![]() $\xi ^{-1}(\mathsf{star}(v))$
is isomorphic to
$\xi ^{-1}(\mathsf{star}(v))$
is isomorphic to
![]() $\Gamma _i$
for some
$\Gamma _i$
for some
![]() $i=1,2$
for every
$i=1,2$
for every
![]() $v\in K$
. Corollary 6.4 implies that
$v\in K$
. Corollary 6.4 implies that
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
are both
$\Gamma _2$
are both
![]() $k$
-fillable for some
$k$
-fillable for some
![]() $k$
. Then Proposition 6.6 implies that
$k$
. Then Proposition 6.6 implies that
![]() $\Gamma$
is
$\Gamma$
is
![]() $k$
-fillable and
$k$
-fillable and
Then Corollary 6.4 implies that
On the other hand, the properties of the morphism
![]() $\Gamma \to T$
imply that there is a retraction
$\Gamma \to T$
imply that there is a retraction
![]() $\Gamma \to \Gamma _i$
and hence Proposition 6.5 implies that
$\Gamma \to \Gamma _i$
and hence Proposition 6.5 implies that
![]() $f_k^{\Gamma _i} \preceq f_k^\Gamma$
and therefore
$f_k^{\Gamma _i} \preceq f_k^\Gamma$
and therefore
![]() $ \Delta _i \preceq \Delta .$
$ \Delta _i \preceq \Delta .$
Acknowledgements
We thank the referee for feedback and corrections. The authors also thank Sam Hughes for comments in a preliminary version of the article. The authors also thank Tomohiro Fukaya and Takumi Matsuda for comments on the manuscript. The first author acknowledges funding by the Fonds de Recherche du Québec-Nature et Technologies FRQNT. The second author acknowledges funding by the Natural Sciences and Engineering Research Council of Canada NSERC.