Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-15T19:51:26.136Z Has data issue: false hasContentIssue false
  • English
  • Français

A remark on a conjecture of Marcus on the generalized numerical range

Published online by Cambridge University Press:  18 May 2009

Yik-Hoi Au-Yeung  and
Kam-Chuen Ng
Yik-Hoi Au-Yeung
Affiliation:
Department Of Mathematics, University Of Hong Kong
Kam-Chuen Ng
Affiliation:
Department Of Mathematics, University Of Hong Kong
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be an n × n complex matrix and c = (c1… cn) єℂn. Define the c-numerical range of A to be the set 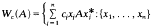is an orthonormal set in 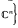, where * denotes the conjugate transpose. Westwick [8[ proved that if c … cn are collinear, then Wc(A) is convex. (Poon [6] gave another proof.) But in general for n ≧3, Wc(A) may fail to be convex even for normal A (for example, see Marcus [4] or Lemma 3 in this note) though it is star-shaped (Tsing [7]). In the following, we shall assume that A is normal. Let W(A) = {diag UAU*: U is unitary}. Horn [3] proved that if the eigenvalues of A are collinear, then W(A) is convex. Au-Yeung and Sing [2] showed that the converse is also true. Marcus [4] further conjectured (and proved for n = 3) that if Wc(A) is convex for all cєℂn then the eigenvalues of A are collinear. Let λ = (λ1, …, λn єℂn. We denote by 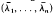the vector λ1, …, λn and by [λ] the diagonal matrix with λ1, …, λn lying on its diagonal. Since, for any unitary matrix U,. Wc(A) = Wc (UAU*), the Marcus conjecture reduces to: if Wc([λ]) is convex for all c єℂn then λ1, … λn are collinear. For the case n = 3, Au-Yeung and Poon [1] gave a complete characterization on the convexity of the set Wc([λ]) in terms of the relative position of the points 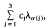, where σ є S3 the permutation group of order 3. As an example they showed that if λ1, λ2, λ3 are not collinear, then 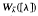is not convex (Lemma 3 in this note gives another proof). We shall show that for the case n = 4, 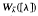is not convex if λ1, λ2. λ3. λ4 are not collinear. Thus for n = 3, 4 the Marcus conjecture is answered and improved.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 24 , Issue 2 , July 1983 , pp. 191 - 194
Copyright
Copyright © Glasgow Mathematical Journal Trust 1983

References

REFERENCES

1.Au-Yeung, Y. H. and Poon, Y. T., 3 × 3 orthostochastic matrices and the convexity of generalized numerical ranges, Linear Algebra and Appl. 27 (1979), 69–79.CrossRefGoogle Scholar
2.Au-Yeung, Y. H. and Sing, F. Y., A remark on the generalized numerical range of a normal matrix, Glasgow Math. J. 18 (1977), 179–180.CrossRefGoogle Scholar
3.Horn, A., Doubly stochastic matrices and the diagonal of a rotation matrix, Amer. J. Math. 76 (1954), 620–630.CrossRefGoogle Scholar
4.Marcus, M., Some combinatorial aspects of numerical range, Ann. New York Acad. Sci. 319 (1979), 368–376.CrossRefGoogle Scholar
5.Mirsky, L., Proofs of two theorems on doubly-stochastic matrices, Proc. Amer. Math. Soc. 9 (1958), 371–374.CrossRefGoogle Scholar
6.Poon, Y. T., Another proof of a result of Westwick, Linear and Multilinear Algebra 9 (1980), 35–37.CrossRefGoogle Scholar
7.Tsing, N. K., On the shape of the generalized numerical ranges, Linear and Multilinear Algebra 10 (1981), 173–182.CrossRefGoogle Scholar
8.Westwick, R., A theorem on numerical range, Linear and Multilinear Algebra 2 (1975), 311–315.CrossRefGoogle Scholar