Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mirsky, L
1969.
Transversal theory and the study of abstract independence.
Journal of Mathematical Analysis and Applications,
Vol. 25,
Issue. 1,
p.
209.
1971.
An account of some aspects of combinatorial mathematics.
Vol. 75,
Issue. ,
p.
236.
Perfect, Hazel
1980.
Remarks on Dilworth's theorem in relation to transversal theory.
Glasgow Mathematical Journal,
Vol. 21,
Issue. 1,
p.
19.
Anderson, I.
1985.
Counting common representatives and symmetric chain decompositions.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 100,
Issue. 1-2,
p.
151.
Hsu, Tim
Logan, Mark J.
and
Shahriari, Shahriar
2009.
Methods for nesting rank 3 normalized matching rank-unimodal posets.
Discrete Mathematics,
Vol. 309,
Issue. 3,
p.
521.
Farley, Jonathan David
2023.
Perfect Solutions to Problems on Common Transversals and Submodular Functions from Welsh’s 1976 Text Matroid Theory.
Mathematica Pannonica,
Vol. 29_NS3,
Issue. 1,
p.
8.

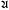 = (
= (