Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Alías, Luis J.
García-Martínez, S. Carolina
and
Rigoli, Marco
2012.
A maximum principle for hypersurfaces with constant scalar curvature and applications.
Annals of Global Analysis and Geometry,
Vol. 41,
Issue. 3,
p.
307.
Alías, Luis J.
Mastrolia, Paolo
and
Rigoli, Marco
2016.
Maximum Principles and Geometric Applications.
p.
325.
Alías, Luis J.
Meléndez, Josué
and
Palmas, Oscar
2018.
Hypersurfaces with constant scalar curvature in space forms.
Differential Geometry and its Applications,
Vol. 58,
Issue. ,
p.
65.
DE LIMA, EUDES L.
and
DE LIMA, HENRIQUE F.
2020.
COMPLETE WEINGARTEN HYPERSURFACES SATISFYING AN OKUMURA TYPE INEQUALITY.
Journal of the Australian Mathematical Society,
Vol. 109,
Issue. 1,
p.
81.
Meléndez, Josué
and
Palmas, Oscar
2022.
Rigidity of hypersurfaces with constant higher order mean curvature in space forms.
Boletín de la Sociedad Matemática Mexicana,
Vol. 28,
Issue. 2,
de Lima, Eudes L.
and
de Lima, Henrique F.
2022.
A gap theorem for constant scalar curvature hypersurfaces.
Collectanea Mathematica,
Vol. 73,
Issue. 1,
p.
1.

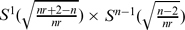 and
and 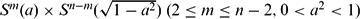 in a unit sphere
in a unit sphere 