Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T07:15:26.810Z Has data issue: false hasContentIssue false
  • English
  • Français

ROUNDNESS PROPERTIES OF ULTRAMETRIC SPACES

Published online by Cambridge University Press:  13 August 2013

TIMOTHY FAVER ,
KATELYNN KOCHALSKI ,
MATHAV KISHORE MURUGAN ,
HEIDI VERHEGGEN ,
ELIZABETH WESSON  and
ANTHONY WESTON
TIMOTHY FAVER
Affiliation:
Department of Mathematics, Drexel University, Philadelphia, PA 19104, USA e-mail: tef@drexel.edu
KATELYNN KOCHALSKI
Affiliation:
Department of Mathematics, University of Virginia, Charlottesville, VA 22904, USA e-mail: kdk7rn@virginia.edu
MATHAV KISHORE MURUGAN
Affiliation:
Center for Applied Mathematics, Cornell University, Ithaca, NY 14853, USA email: mkm233@cornell.edu
HEIDI VERHEGGEN
Affiliation:
Department of Economics, Cornell University, Ithaca, NY 14853, USA e-mail: hv59@cornell.edu
ELIZABETH WESSON
Affiliation:
Center for Applied Mathematics, Cornell University, Ithaca, NY 14853, USA e-mail: enw27@cornell.edu
ANTHONY WESTON
Affiliation:
Department of Mathematics and Statistics, Canisius College, Buffalo, NY 14208, USAwestona@canisius.edu Department of Decision Sciences, University of South Africa, PO Box 392, UNISA 0003, South Africawestoar@unisa.ac.za
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Motivated by a classical theorem of Schoenberg, we prove that an n + 1 point finite metric space has strict 2-negative type if and only if it can be isometrically embedded in the Euclidean space 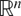$\mathbb{R}^{n}$ of dimension n but it cannot be isometrically embedded in any Euclidean space 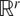$\mathbb{R}^{r}$ of dimension r < n. We use this result as a technical tool to study ‘roundness’ properties of additive metrics with a particular focus on ultrametrics and leaf metrics. The following conditions are shown to be equivalent for a metric space (X,d): (1) X is ultrametric, (2) X has infinite roundness, (3) X has infinite generalized roundness, (4) X has strict p-negative type for all p ≥ 0 and (5) X admits no p-polygonal equality for any p ≥ 0. As all ultrametric spaces have strict 2-negative type by (4) we thus obtain a short new proof of Lemin's theorem: Every finite ultrametric space is isometrically embeddable into some Euclidean space as an affinely independent set. Motivated by a question of Lemin, Shkarin introduced the class 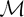$\mathcal{M}$ of all finite metric spaces that may be isometrically embedded into ℓ2 as an affinely independent set. The results of this paper show that Shkarin's class 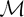$\mathcal{M}$ consists of all finite metric spaces of strict 2-negative type. We also note that it is possible to construct an additive metric space whose generalized roundness is exactly ℘ for each ℘ ∈ [1, ∞].

Keywords

54E4046C0551K05
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 56 , Issue 3 , September 2014 , pp. 519 - 535
Copyright
Copyright © Glasgow Mathematical Journal Trust 2013 

References

REFERENCES

1.Bartal, Y., Linial, N., Mendel, M. and Naor, A., On metric Ramsey-type phenomena, Proceedings of the 35th Annual ACM Symposium on Theory of Computing (ACM, San Diego, CA, 2003), 463–472.Google Scholar
2.Bartal, Y., Linial, N., Mendel, M. and Naor, A., Low dimensional embeddings of ultrametrics, Eur. J. Comb. 25 (2004), 87–92.CrossRefGoogle Scholar
3.Blumenthal, L. M., Theory and applications of distance geometry, 2nd ed. (Chelsea Publishing, New York, 1970).Google Scholar
4.Bourgain, J., Milman, V. and Wolfson, H., On type of metric spaces, Trans. Amer. Math. Soc. 294 (1986), 295–317.Google Scholar
5.Buneman, P., A note on the metric properties of trees, J. Comb. Theory B 17 (1974), 48–50.CrossRefGoogle Scholar
6.Caffarelli, E., Doust, I. and Weston, A., Metric trees of generalized roundness one, Aeq. Math. 83 (2012), 239–256.Google Scholar
7.de Groot, J., Non-Archimedean metrics in topology, Proc. Amer. Math. Soc. 7 (1956), 948–953.Google Scholar
8.Dekster, B. V. and Wilker, J. B., Edge lengths guaranteed to form a simplex, Arch. Math. 49 (1987), 351–366.Google Scholar
9.Deza, M. and Maehara, H., Metric transforms and Euclidean embeddings, Trans. Amer. Math. Soc. 317 (1990), 661–671.Google Scholar
10.Diestel, J., Jarchow, H. and Tonge, A. M., Absolutely summing operators, Cambridge Studies in Advanced Mathematics, vol. 43 (Cambridge University Press, Cambridge, UK, 1995), 1–474.CrossRefGoogle Scholar
11.Doust, I. and Weston, A., Enhanced negative type for finite metric trees, J. Funct. Anal. 254 (2008), 2336–2364.CrossRefGoogle Scholar
12.Enflo, P., On the nonexistence of uniform homeomorphisms between Lp-spaces, Ark. Mat. 8 (1968), 103–105.Google Scholar
13.Enflo, P., On a problem of Smirnov, Ark. Mat. 8 (1969), 107–109.Google Scholar
14.Enflo, P., Uniform structures and square roots in topological groups I, Israel J. Math. 8 (1970), 230–252.Google Scholar
15.Enflo, P., Uniform structures and square roots in topological spaces II, Israel J. Math. 8 (1970), 253–272.Google Scholar
16.Fakcharoenphol, J., Rao, S. and Talwar, K., A tight bound on approximating arbitrary metrics by tree metrics, in Proceedings of the 35th Annual ACM Symposium on Theory of Computing (ACM, San Diego, CA, 2003) 448–455.Google Scholar
17.Fiedler, M., Ultrametric sets in Euclidean point spaces, Elecron. J. Linear Algebr. 3 (1998), 23–30.Google Scholar
18.Gordon, A. D., A review of hierarchical classification, J. Roy. Statist. Soc. A 150 (1987), 119–137.CrossRefGoogle Scholar
19.Higson, N. and Roe, J., On the coarse Baum–Connes conjecture, in Novikov Conjectures, Index Theorems, and Rigidity (Ferry, S. C., Ranicki, A. and Rosenberg, J. M., Editors), Lond. Math. Soc. Lecture Note Series, vol. 227 (Cambridge University Press, Cambridge, UK, 1995), 227–254.Google Scholar
20.Hjorth, P. G., Kokkendorff, S. L. and Markvorsen, S., Hyperbolic spaces are of strictly negative type, Proc. Amer. Math. Soc. 130 (2002), 175–181.Google Scholar
21.Hjorth, P., Lisoněk, P., Markvorsen, S. and Thomassen, C., Finite metric spaces of strictly negative type, Linear Algebr. Appl. 270 (1998), 255–273.CrossRefGoogle Scholar
22.Holly, J. E., Pictures of ultrametric spaces, the p-adic numbers, and valued fields, Am. Math. Mon. 108 (2001), 721–728.CrossRefGoogle Scholar
23.Hughes, B., Trees and ultrametric spaces: A categorical equivalence, Adv. Math. 189 (2004), 148–191.CrossRefGoogle Scholar
24.Hughes, B., Trees, ultrametrics and noncommutative geometry, Pure Appl. Math. Q. 8 (2012), 221–312.CrossRefGoogle Scholar
25.Kelleher, C., Miller, D., Osborn, T. and Weston, A., Polygonal equalities and virtual degeneracy in Lp-spaces, preprint (arXiv:1203.5837).Google Scholar
26.Kelly, J. B., Metric inequalities and symmetric differences, in Inequalities-II (Shisha, O., Editor) (Academic Press, New York, 1970), 193–212.Google Scholar
27.Kelly, J. B., Hypermetric spaces and metric transforms, in Inequalities-III (Shisha, O., Editors) (Academic Press, New York, 1972), 149–158.Google Scholar
28.Lafont, J-F. and Prassidis, S., Roundness properties of groups, Geom. Ded. 117 (2006), 137–160.Google Scholar
29.Lemin, A. J., Isometric embedding of isosceles (non-Archimedean) spaces in Euclidean spaces, Soviet Math. Dokl. 32 (3) (1985), 740–744.Google Scholar
30.Lennard, C. J., Tonge, A. M. and Weston, A., Generalized roundness and negative type, Michigan Math. J. 44 (1997), 37–45.Google Scholar
31.Li, H. and Weston, A., Strict p-negative type of a metric space, Positivity 14 (2010), 529–545.Google Scholar
32.Mendel, M. and Naor, A., Scaled Enflo type is equivalent to Rademacher type, Bull. Lond. Math. Soc. 39 (2007), 493–498.Google Scholar
33.Menger, K., Die Metrik des Hilbert-Raumes, Akad. Wiss. Wien Abh. Math.-Natur. K1 65 (1928), 159–160.Google Scholar
34.Menger, K., Untersuchungen úber allgemeine Metrik, Math. Ann. 100 (1928), 75–163.CrossRefGoogle Scholar
35.Michon, G., Les Cantors réguliers, C. R. Acad. Sci. Paris Sér. I Math. 300 (1985), 673–675.Google Scholar
36.Naor, A. and Schechtman, G., Remarks on non linear type and Pisier's inequality, J. Reine Angew. Math. (Crelle's Journal) 552 (2002), 213–236.Google Scholar
37.Nickolas, P. and Wolf, R., Distance geometry in quasihypermetric spaces. III, Math. Nachr. 284 (2011), 747–760.Google Scholar
38.Sánchez, S., On the supremal p-negative type of a finite metric space, J. Math. Anal. Appl. 389 (2012), 98–107.Google Scholar
39.Schoenberg, I. J., Remarks to Maurice Frechet's article `Sur la définition axiomatique d'une classe d'espaces distanciés vectoriellement applicable sur l'espace de Hilbert', Ann. Math. 36 (1935), 724–732.CrossRefGoogle Scholar
40.Schoenberg, I. J., On certain metric spaces arising from Euclidean spaces by a change of metric and their imbedding in Hilbert space, Ann. Math. 38 (1937), 787–793.CrossRefGoogle Scholar
41.Schoenberg, I. J., Metric spaces and positive definite functions, Trans. Amer. Math. Soc. 44 (1938), 522–536.CrossRefGoogle Scholar
42.Shkarin, S. A., Isometric embedding of finite ultrametric spaces in Banach spaces, Topol. Appl. 142 (2004), 13–17.Google Scholar
43.Timan, A. F. and Vestfrid, I. A., Any separable ultrametric space can be isometrically imbedded in ℓ2, Funkt. Anal. i Prilozhen. 17 (1) (1983), 85–86 (in Russian); English transl.: Funct. Anal. Appl. 17 (1983), 70–71.Google Scholar
44.Watson, S., The classification of metrics and multivariate statistical analysis, Topol. Appl. 99 (1999), 237–261.Google Scholar
45.Wells, J. H. and Williams, L. R., Embeddings and extensions in analysis, Ergeb. Math. Grenzgeb., vol. 84 (Springer, Berlin, 1975).Google Scholar
46.Weston, A., On the generalized roundness of finite metric spaces, J. Math. Anal. Appl. 192 (1995), 323–334.CrossRefGoogle Scholar
47.Wolf, R., On the gap of finite metric spaces of p-negative type, Linear Alegbr. Appl. 436 (2012), 1246–1257.CrossRefGoogle Scholar