Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-15T17:50:38.970Z Has data issue: false hasContentIssue false
  • English
  • Français

The semigroup of one-to-one transformations with finite defects

Published online by Cambridge University Press:  18 May 2009

Inessa Levi  and
Boris M. Schein
Inessa Levi
Affiliation:
Department of Mathematics, University of Louisville, Lousville, Kentucky 40292
Boris M. Schein
Affiliation:
Department of Mathematical Sciences, University of Arkansas, Fayetteville, Arkansas 72701
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 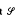be the semigroup of all total one-to-one transformations of an infinite set X. For an ƒ ∈ 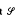let the defect of ƒ def ƒ, be the cardinality of X – R(ƒ), where R(ƒ) = ƒ(X) is the range of ƒ. Then 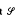is a disjoint union of the symmetric group 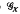x on X, the semigroup S of all transformations in 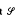with finite non-zero defects and the semigroup Ā of all transformations in S with infinite defects, such that S U Ā and Ā are ideals of 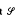. The properties of 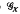x and Ā have been investigated by a number of authors (for the latter it was done via Baer-Levi semigroups, see [2], [3], [5], [6], [7], [8], [9], [10] and note that Ā decomposes into a union of Baer–Levi semigroups). Our aim here is to study the semigroup S. It is not difficult to see that S is left cancellative (we compose functions ƒ, g in S as ƒg(x) = ƒ(g(x)), for x ∈ X) and idempotent-free. All automorphisms of S are inner [4], that is of the form ƒ → hƒhfh-1 ƒ ∈ S, h ∈ 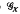x.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 31 , Issue 2 , May 1989 , pp. 243 - 249
Copyright
Copyright © Glasgow Mathematical Journal Trust 1989

References

1.Clifford, A. H. and Preston, G. B., Algebraic theory of semig roups, Math Surveys No. 7, Amer. Math. Soc, Providence, R.I., Vol. I (1961).Google Scholar
2.Levi, I., Schein, B. M., Sullivan, R. P. and Wood, G. R., Automorphisms of Baer-Levi semigroups, J. London Math. Soc. (2) 28 (1983), 492–495.CrossRefGoogle Scholar
3.Levi, I. and Wood, G. R., On maximal subsemigroups of Baer-Levi semigroups, Semigroup Forum, 30 (1984), 99–102.Google Scholar
4.Levi, I., Automorphisms of normal transformation semigroups, Proc. Edinburgh Math. Soc., 28 (1985), 185–205.CrossRefGoogle Scholar
5.Lindsey, D. and Madison, B., The lattice of congruences on Baer-Levi semigroup, Semigroup Forum 12 (1976), 63–70.CrossRefGoogle Scholar
6.Mielke, B. W., Regular congruences on Croisot-Teissier and Baer-Levi semigroups, J. Math. Soc. Japan 24 (1972), 539–551.CrossRefGoogle Scholar
7.Mielke, B. W., Regular congruences on a simple semigroup with a minimal right ideal, Publ. Math. Debreceen 20 (1973), 79–84.CrossRefGoogle Scholar
8.Mielke, B. W., Completely simple congruences on Croisot-Teissier semigroups, Semigroup Forum 9 (1975), 283–293.Google Scholar
9.Schein, B. M., Symmetric semigroups of one-to-one transformations, Second all-union symposium on the theory of semigroups, summaries of talks, Sverdlovsk (1979), 99 (Russian).Google Scholar
10.Shutov, E. G., Semigroups of one-to-one transformations, Dokl. Akad. Nauk. SSSR 140 (1961), 1026–1028.Google Scholar