Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nystedt, Patrik
and
Öinert, Johan
2015.
Simple semigroup graded rings.
Journal of Algebra and Its Applications,
Vol. 14,
Issue. 07,
p.
1550102.
Gordienko, Alexey
and
Schnabel, Ofir
2018.
On weak equivalences of gradings.
Journal of Algebra,
Vol. 501,
Issue. ,
p.
435.
Gordienko, Alexey
and
Schnabel, Ofir
2019.
Categories and Weak Equivalences of Graded Algebras.
Algebra Colloquium,
Vol. 26,
Issue. 04,
p.
643.

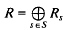 be an
be an 