Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-15T09:32:13.010Z Has data issue: false hasContentIssue false
  • English
  • Français

Semigroups of non-negative integral matrices

Published online by Cambridge University Press:  18 May 2009

Craig M. Cordes
Craig M. Cordes
Affiliation:
Louisiana State University, Baton Rouge, Louisiana 70803
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [1], Pall proved an interesting result on a certain class of 2 × 2 integral matrices. He showed that the semigroup of 2 × 2 matrices of determinant 1 and non-negative entries contains exactly 2 primes 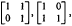, and every other non-unit is expressible uniquely as products of these primes. Before formally stating this result, we need some notation. Let Gn denote the semigroup of n × n matrices with determinant 1 and nonnegative integral entries, In the n × n identity matrix, 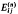the n × n matrix with a 1 as its (i, j) element and zeros elsewhere, and let 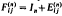. When the dimension is clear, we shall drop the superscripts.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 15 , Issue 1 , March 1974 , pp. 39 - 42
Copyright
Copyright © Glasgow Mathematical Journal Trust 1974

References

REFERENCE

1.Pall, Gordon, Binary quadratic and cubic forms and unipositive matrices; to appear in J. Number Theory.Google Scholar