Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T06:16:28.365Z Has data issue: false hasContentIssue false
  • English
  • Français

SIGN CHANGES OF FOURIER COEFFICIENTS OF ENTIRE MODULAR INTEGRALS

Published online by Cambridge University Press:  29 March 2012

YOUNGJU CHOIE  and
WINFRIED KOHNEN
YOUNGJU CHOIE
Affiliation:
Department of Mathematics, Pohang Institute of Science and Technology and Pohang Mathematical Institute (PMI), Pohang 790-784, Korea e-mail: yjc@postech.ac.kr
WINFRIED KOHNEN
Affiliation:
Mathematisches Institut der Universität, INF 288, D-69120 Heidelberg, Germany e-mail: winfried@mathi.uni-heidelberg.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let f be a non-zero cusp form with real Fourier coefficients a(n) (n ≥ 1) of positive real weight k and a unitary multiplier system v on a subgroup Γ ⊂ SL2(ℝ) that is finitely generated and of Fuchsian type of the first kind. Then, it is known that the sequence (a(n))(n ≥ 1) has infinitely many sign changes. In this short note, we generalise the above result to the case of entire modular integrals of non-positive integral weight k on the group Γ0*(N) (N ∈ ℕ) generated by the Hecke congruence subgroup Γ0(N) and the Fricke involution 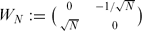provided that the associated period functions are polynomials.

Keywords

Primary 11F0311F99
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 54 , Issue 2 , May 2012 , pp. 355 - 358
Copyright
Copyright © Glasgow Mathematical Journal Trust 2012

References

REFERENCES

1.Bol, G., Invarianten linearer differential gleichungen, Abh. Math. Sem. Univ. Hamburg. 16 (3–4) (1949), 1–28.Google Scholar
2.Knopp, M., Modular integrals on Γ0(N) and Dirichlet series with functional equations, in Number theory (Chudnovsky, D. V. et al. Editors) (Springer, Berlin, Germany, 1985), 211–224. Lect. No. 1135.CrossRefGoogle Scholar
3.Knopp, M., Kohnen, W. and Pribitkin, W., On the signs of Fourier coefficients of cusp forms, Ramanujan J. 7 (2003), 269–277.CrossRefGoogle Scholar
4.Kohnen, W., On the growth of the Petersson norms of Fourier-Jacobi coefficients of Siegel cusp forms, Bull. Lond. Math. Soc. 43 (4) (2011), 717–720.CrossRefGoogle Scholar
5.Landau, E., Uber einen Satz von Tschebyschef, Math. Ann. 61 (1906), 527–550.CrossRefGoogle Scholar