Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-15T05:48:09.634Z Has data issue: false hasContentIssue false
  • English
  • Français

Singular pleated surfaces and CP1–structures

Published online by Cambridge University Press:  18 May 2009

Ser Peow Tan
Ser Peow Tan
Affiliation:
Department of Mathematics, Faculty of Science, National University of Singapore, 10 Kent Ridge Crescent, Singapore, 0511, e-mail: mattansp@lecnis.nus.sg
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Fg be a closed orientable surface of genus g > 1 and let 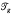be the Teichmuller space of Fg, i.e., the space of marked hyperbolic structures on Fg We shall also denote by 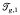the space of marked hyperbolic structures on Fgwith one distinguished point; by this, we mean a distinguished point on the universal cover 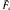gof Fg. This space is isomorphic to the space of marked complete hyperbolic structures on a genus g surface with 1 cusp which is the usual interpretation of 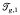. Choose a decomposition of Fginto pairs of pants by a collection of non–intersecting, totally geodesic simple closed curves. The Fenchel–Nielsen coordinates for 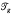relative to this decomposition are given by the lengths of the curves as well as twist parameters defined on each curve. Varying the length and twist parameters gives deformations of the marked hyperbolic structures.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 37 , Issue 2 , May 1995 , pp. 179 - 190
Copyright
Copyright © Glasgow Mathematical Journal Trust 1995

References

REFERENCES

1.Apanasov, B., Kobayashi conformal metrics on manifolds, Chern–Simons and eta invariants, International J. Math., 2:4 (1991), 361–382.CrossRefGoogle Scholar
2.Apanasov, B., Deformations of Conformal Structures on hyperbolic manifolds, J. Differential Geometry 35 (1992), 1–20.CrossRefGoogle Scholar
3.Apanasov, B. and Tetenov, A., Deformations of hyperbolic structures along pleated surfaces, preprint, (1992).Google Scholar
4.Ballmann, W., Gromov, M. and Schroeder, V., Manifolds of non-positive curvature (Birkhauser, 1985).CrossRefGoogle Scholar
5.Beardon, A., The geometry of discrete groups (Springer–Verlag, 1983).CrossRefGoogle Scholar
6.Epstein, D. B. A. and Marden, A., Convex hulls in hyperbolic spaces, A theorem of Sullivan and measured pleated surfaces, London Math. Soc. Lecture Notes Series No. Ill (1987), 113–254.Google Scholar
7.Goldman, W. M., Projective structures with Fuchsian holonomy, J. Differential Geometry 25 (1987), 297–326.CrossRefGoogle Scholar
8.Gromov, M., Lawson, H. B. and Thurston, W., Hyperbolic 4–manifolds and conformally flat 3–manifolds, Publ. Math. Inst. Hautes Etudes Sci. 68 (1988), 27–45.CrossRefGoogle Scholar
9.Johnson, D. and Millson, J. J., Deformation spaces associated to compact hyperbolic manifolds, in Discrete Groups in Geometry and analysis; Papers in Honor of G. D. Mostow on His Sixtieth Birthday. Howe, R. (ed.), Progress in Math. 67 (Birkhauser, 1987), 48–106.Google Scholar
10.Kamishima, Y. and Tan, S. P., Deformation Spaces associated to Geometric Structures, Advanced Studies in Pure Mathematics 20 (1991), 1–37.Google Scholar
11.Kapovich, M., On deformations of representations of discrete cocompact subgroups of SO(3,1), preprint.Google Scholar
12.Kourouniotis, C., Deformations of hyperbolic structures on manifolds of several dimensions, Math. Proc. Camb. Phil. Soc. 98 (1985), 247–261.CrossRefGoogle Scholar
13.Kulkarni, R. S. and Pinkall, U., A Canonical Metric for Moebius Structures and Its Applications, preprint, (1991).Google Scholar
14.Morgan, J. and Shalen, P., Valuations, trees and degenerations of hyperbolic structures I, Ann. of Math. 120(1984), 401–476.CrossRefGoogle Scholar
15.Penner, R. C., The Decorated Teichmuller Space of Punctured Surfaces, Commun. Math. Phys. 113, (1987), 299–339.CrossRefGoogle Scholar
16.Tan, S. P., Deformations of flat conformal structures on a hyperbolic 3–manifold, J. Differential Geometry 37 (1993), 161–177.CrossRefGoogle Scholar
17.Tan, S. P., Conformally flat 3–manifolds and Euclidean polyhedra, Communications in Analysis and Geometry, to appear.Google Scholar
18.Thurston, W. P., The Geometry and Topology of three–manifolds, Princeton University Mathematics Department notes (1979).Google Scholar
19.Thurston, W. P., Shapes of Polyhedra, Research Report GCG 7, Geometry Supercomputer Project.Google Scholar