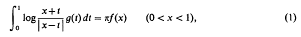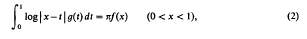Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Parihar, K. S.
1971.
XIX.—Some Triple Trigonometrical Series Equations and their Application.
Proceedings of the Royal Society of Edinburgh. Section A. Mathematical and Physical Sciences,
Vol. 69,
Issue. 3,
p.
255.
Srivastava, H.M
1972.
A pair of dual series equations involving generalized Bateman k-functions.
Indagationes Mathematicae (Proceedings),
Vol. 75,
Issue. 1,
p.
53.
Leppington, F. G.
and
Levine, H.
1972.
Some axially symmetric potential problems.
Proceedings of the Edinburgh Mathematical Society,
Vol. 18,
Issue. 1,
p.
55.
Williams, W. E.
1972.
A note on integral equations.
Glasgow Mathematical Journal,
Vol. 13,
Issue. 2,
p.
119.
Kelman, Robert B.
and
Koper, Chester A.
1973.
Least squares approximations for dual trigonometric series.
Glasgow Mathematical Journal,
Vol. 14,
Issue. 2,
p.
111.
Homentcovschi, D.
1974.
On an integral equation.
Glasgow Mathematical Journal,
Vol. 15,
Issue. 2,
p.
95.
Kelman, Robert B.
and
Timothy Simpson, J.
1975.
An algorithm for solving a dual cosine series.
Computers & Mathematics with Applications,
Vol. 1,
Issue. 2,
p.
195.
Evans, D. V.
1975.
A note on the total reflexion or transmission of surface waves in the presence of parallel obstacles.
Journal of Fluid Mechanics,
Vol. 67,
Issue. 3,
p.
465.
Kelman, Robert B.
Maheffy, Johnathan P.
and
Simpson, J.Timothy
1977.
Algorithms for classic dual trigonometric equations.
Computers & Mathematics with Applications,
Vol. 3,
Issue. 3,
p.
203.
Singh, Brij M.
and
Dhaliwal, Ranjit S.
1979.
Dual integral equations with a trigonometric Kernel.
Proceedings of the Edinburgh Mathematical Society,
Vol. 22,
Issue. 3,
p.
213.
Lowndes, J. S.
and
Meister, E.
1980.
The solution of some integral equations.
Mathematical Methods in the Applied Sciences,
Vol. 2,
Issue. 1,
p.
26.
Singh, B. M.
and
Bryant Moodie, T.
1981.
Closed-form solutions for finite length crack moving in a strip under anti-plane shear stress.
Acta Mechanica,
Vol. 38,
Issue. 1-2,
p.
99.
Singh, B.M
Rokne, Jon G
and
Dhaliwal, R.S
1981.
A contact problem for a nonhomogeneous half-space.
International Journal of Engineering Science,
Vol. 19,
Issue. 3,
p.
427.
Shail, R.
1981.
A note on neumann potential problems for a thin circular annulus.
International Journal of Engineering Science,
Vol. 19,
Issue. 1,
p.
11.
Mastrojannis, E.N.
Kermanidis, T.B.
and
Mastrogiannis, Arg.
1982.
On the problem of two collinear external line cracks.
International Journal of Engineering Science,
Vol. 20,
Issue. 12,
p.
1353.
Shail, R.
1984.
A class of singular integral equations with some applications.
International Journal of Mathematical Education in Science and Technology,
Vol. 15,
Issue. 3,
p.
359.
Chakrabarti, A.
1989.
Solution of Two Singular Integral Equations Arising in Water Wave Problems.
ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik,
Vol. 69,
Issue. 12,
p.
457.
Lowndes, John S
and
Srivastava, H.M
1990.
Some triple series and triple integral equations.
Journal of Mathematical Analysis and Applications,
Vol. 150,
Issue. 1,
p.
181.
Mandal, B.N.
and
Kundu, P.K.
1991.
A note on the transmission of oblique waves through small apertures.
Computers & Mathematics with Applications,
Vol. 21,
Issue. 4,
p.
17.
Das, A. N.
1993.
Three co-planar moving Griffith cracks in an infinite elastic medium.
International Journal of Fracture,
Vol. 59,
Issue. 4,
p.
291.