Some continuity properties of linear transformations in normed spaces

Extract

Let X and Y be normed spaces and let L(X, Y) denote the set of linear transformations (henceforth called “operators”) T with domain a linear subspace D(T) of X and range R(T) contained in Y. The restriction of T to a subspace E is denoted by T/E; by the usual convention T|E = T|E∩ D(T). For a given linear subspace E the family of infinite dimensional ssubspaces of E is denoted by 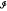(E). An operator Tis said to have a certain property ℙ ubiquitously if every E ∈ 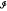(X) contains an F ∈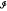(E) for which T|F has property ℙ For example, T is ubiquitously continuous if each E ∈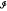(X) contains an F∈ 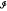(E) for which T|F is continuous. In the present note we shall characterize ubiquitous continuity, isomorphy, precompactness and smallness. A subspace of X is called a principal subspace if it is closed and of finite codimension in X. The restriction of an operator to a principal subspace will be called a principal restriction. The symbol T will always denote an arbitrary operator in L(X, Y).