Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Srivastava, H M
1987.
Neumann expansions for a certain class of generalised multiple hypergeometric series arising in physical and quantum chemical applications.
Journal of Physics A: Mathematical and General,
Vol. 20,
Issue. 4,
p.
847.

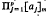 , where [λ]
, where [λ]