Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-15T12:55:28.722Z Has data issue: false hasContentIssue false
  • English
  • Français

Some isometric characterizations of ln∞

Published online by Cambridge University Press:  18 May 2009

Jiang Zhu
Jiang Zhu
Affiliation:
Department of Mathematics, Lancaster University, Lancaster
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The previous results on isometrically characterizing ln∞ in terms of operator ideal norms can be summarized as follows.

Let E be an n-dimensional Banach space.

(1) If λ(E) = 1, then 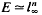(see [3], [5], [6]), where λ(E) is the projection constant of E (see [4]).

(2) If π(E) = n, then 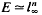(see [1],[2]).

(3) If Δ2(E) = √n, then 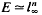(see [8]), where Δ2(E) is the 2-dominated constant of E(see [4]).

(4) If for any linear operator T: → E, v1(T) = 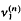(T), then 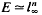(see [7]), where v1 is the 1-nuclear norm (see [4]).

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 34 , Issue 1 , January 1992 , pp. 117 - 121
Copyright
Copyright © Glasgow Mathematical Journal Trust 1992

References

REFERENCES

1.Deschaseaux, J. P., Une caractérisation de certains espaces vectoriels normés de dimension finie par leur constante de Macphail, C. R. Acad. Sci. Paris Sér. A–B 276 (1973), A1349–A1351.Google Scholar
2.Garling, D. J. H., Operators with large trace, and a characterization of l n∞, Proc. Cambridge Philos. Soc. 76 (1974), 413–414.CrossRefGoogle Scholar
3.Goodner, D. B., Projections on normed linear spaces, Trans. Amer. Math. Soc. 69 (1950), 89–108.CrossRefGoogle Scholar
4.Jameson, G. J. O., Summing and nuclear norms in Banach space theory (Cambridge University Press, 1987).CrossRefGoogle Scholar
5.Kelley, J. L., Banach spaces with the extension property, Trans. Amer. Math. Soc. 72 (1952), 323–326.CrossRefGoogle Scholar
6.Nachbin, L., A theorem of the Hahn-Banach type for linear transformations, Trans. Amer. Math. Soc. 68 (1950), 28–46.CrossRefGoogle Scholar
7.Pelczynski, A. and Tomczak-Jaegermann, N., On the length of faithful nuclear representation of finite rank operators, Mathematika 35 (1988), 126–134.CrossRefGoogle Scholar
8.Tomczak-Jaegermann, N., Banach-Mazur distances and finite-dimensional operator ideals (Pitman, 1988).Google Scholar