Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T07:04:21.106Z Has data issue: false hasContentIssue false
  • English
  • Français

SUBPROJECTIVITY OF PROJECTIVE TENSOR PRODUCTS OF BANACH SPACES OF CONTINUOUS FUNCTIONS

Part of: Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  31 March 2021

R.M. CAUSEY
R.M. CAUSEY*
Affiliation:
Independent Scholar, e-mail: rmcausey1701@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Galego and Samuel showed that if K, L are metrizable, compact, Hausdorff spaces, then 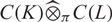$C(K)\widehat{\otimes}_\pi C(L)$ is c0-saturated if and only if it is subprojective if and only if K and L are both scattered. We remove the hypothesis of metrizability from their result and extend it from the case of the twofold projective tensor product to the general n-fold projective tensor product to show that for any 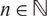$n\in\mathbb{N}$ and compact, Hausdorff spaces K1, …, Kn, 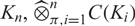$\widehat{\otimes}_{\pi, i=1}^n C(K_i)$ is c0-saturated if and only if it is subprojective if and only if each Ki is scattered.

MSC classification

Primary: 46B03: Isomorphic theory (including renorming) of Banach spaces
Secondary: 46B28: Spaces of operators; tensor products; approximation properties
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 64 , Issue 2 , May 2022 , pp. 292 - 305
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Causey, R. M., The Szlenk index of convex hulls and injective tensor products, J. Funct. Anal. 272(2) (2017), 3375–3409.CrossRefGoogle Scholar
Causey, R. M., Szlenk and weak*-dentability indices of C(K), J. Math. Anal. Appl. 447(2) (2016), 834–845.CrossRefGoogle Scholar
Causey, R. M., Power type ξ-Asymptotically uniformly smooth and ξ-asymptotically uniformly flat norms, J. Math. Anal. Appl. 462(2), (2018), 1482–1518.CrossRefGoogle Scholar
Causey, R. M. and Dilworth, S. J., Higher projective tensor products of c 0, preprint.Google Scholar
Causey, R. M., Galego, E. and Samuel, C., The Szlenk index of $C(K)\widehat{\otimes}_\pi C(L)$ , preprint.Google Scholar
Dáaz, S. and Fernández, A., Reflexivity in Banach lattices. Arch. Math. 63 (1994), 549–552.[8] J. Diestel. A survey ofCrossRefGoogle Scholar
Galego, E. and Samuel, C., The subprojectivity of the projective tensor product of two C(K) spaces with $|K|=\aleph _{0}$ , Proc. Amer. Math. Soc. 144 (2016), 2611–2617.CrossRefGoogle Scholar
Galego, E., González, M. and Pello, J., On Subprojectivity and Superprojectivity of Banach Spaces, Results Math. 71 (2017).CrossRefGoogle Scholar
Grothendieck, A., Sur les applications linéaires faiblement compactes d’espaces du type C(K), Canad. J. Math. 5 (1953), 129–173.Google Scholar
Hájek, P., Lancien, G. and Procházka, A., Weak* dentability index of spaces $C([0,\alpha])$ , J. Math. Anal. Appl. 353 (2009) no. 1, 239–243.CrossRefGoogle Scholar
Lust, F., Produits tensoriels injectifs d’espaces de Sidon, Colloq. Math. 32 (1975), 285–289.CrossRefGoogle Scholar
Oikhberg, T. and Spinu, E., Subprojective Banach spaces, J. Math. Anal. Appl. 424 (2015), 613–635.CrossRefGoogle Scholar
Pełczyński, A. and Semadeni, Z., Spaces of continuous functions (III) (Spaces C(Ω) for Ω without perfect subsets), Studia Math. 18 (1959), 211–222.CrossRefGoogle Scholar
Rudin, W., Continuous Functions on Compact Spaces Without Perfect Subsets, Proc. Amer. Math. Soc. 8(1) (1957), 39–42.CrossRefGoogle Scholar
Ryan, R. A., Introduction to Tensor Products of Banach Spaces, Springer-Verlag, London, (2002).CrossRefGoogle Scholar
Samuel, C., Indice de Szlenk des C(K), Séeminaire de Géométrie des espaces de Banach, Vol. I-II, Publications Mathématiques de l’Universitée Paris VII, Paris (1983) 81–91.Google Scholar
Whitley, R. J., Strictly singular operators and their conjugates. Trans. Amer. Math. Soc. 113 (1964) 252–261.CrossRefGoogle Scholar