Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-15T15:59:00.152Z Has data issue: false hasContentIssue false
  • English
  • Français

Substitutional lemma for G-spaces of 1-dimensional groups

Published online by Cambridge University Press:  18 May 2009

Juan Antonio Pérez
Juan Antonio Pérez
Affiliation:
Centro Regional de Estudios Nucleares, Universidad Autónoma de Zacatecas, Apartado Postal 495, 98068 Zacatecas, Zac., México email;japerez@bufa.cantera
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a compact Lie group and X a G-CW complex. We are interested in the calculation of the Borel cohomology of X

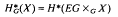
where EG is a universal free G-space and we use on the right hand side cellular cohomology. For an introduction to G-CW complexes see Matumoto [4] and for a good exposition on Borel cohomology see for instance torn Dieck [2], We want to replace X with an ordinary CW complex Y in order to find an ordinary CW structure on the Borel construction EG ΧGY so we can use cellular chains to compute the Borel cohomology of X. For every compact Lie group one has an extension

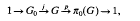
where G0 is the identity component, so for our case G0 is isomorphic to the circle group 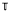. We are dealing with the case in which π0(G) is isomorphic to C2, the cyclic group of order

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 38 , Issue 2 , May 1996 , pp. 215 - 220
Copyright
Copyright © Glasgow Mathematical Journal Trust 1996

References

REFERENCES

1.Brown, K. S., Cohomology of groups (Springer Verlag, 1982).CrossRefGoogle Scholar
2.Dieck, T. torn, Transformation groups. (Walter de Gruyter, 1987).CrossRefGoogle Scholar
3.Greenlees, J. P. C. and May, J. P., Generalized Tate cohomology, Mem. Amer. Math. Soc. (to appear).Google Scholar
4.Matumoto, T., On G-CW complexes and a theorem of J. H. C. Whitehead, J. Fac. Sci. Univ. Tokio 18 (1971) 363–374.Google Scholar