Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-15T15:26:52.191Z Has data issue: false hasContentIssue false
  • English
  • Français

Supersoluble groups of automorphisms of compact Riemann surfaces

Published online by Cambridge University Press:  18 May 2009

Grzegorz Gromadzki  and
Colin MacLachlan
Grzegorz Gromadzki
Affiliation:
Instytut Matematyki WSP, Chodkiewicza 30, 85–064 Bydgoszcz, Poland. and, Universidad a Distancia, Depto de Matem, Fund. 28040 Madrid, Spain.
Colin MacLachlan
Affiliation:
Department of Mathematics, University of Aberdeen, The Edward Wright Building, Dunbar Street, Aberdeen AB9 2TY
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given an integer g ≥ 2 and a class 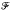of finite groups let N(g, 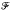) denote the order of the largest group in 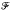that a compact Riemann surface of genus g admits as a group of automorphisms. For the classes of all finite groups, cyclic groups, abelian groups, nilpotent groups, p-groups (given p), soluble groups and finally for metabelian groups, an upper bound for N(g, 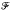) as well as infinite sequences for g for which this bound is attained were found in [5, 6, 7, 8, 13], [4], [10], [15], [16], [1], [2] respectively. This paper deals with that problem for the class of finite supersoluble groups i.e. groups with an invariant series all of whose factors are cyclic. In addition, it goes further by describing exactly those values of g for which the bound is attained. More precisely we prove:

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 31 , Issue 3 , September 1989 , pp. 321 - 327
Copyright
Copyright © Glasgow Mathematical Journal Trust 1989

References

1.Chetiya, B. P., Groups of Automorphisms of compact Riemann surfaces, Ph.D. thesis, Birmingham University.Google Scholar
2.Chetiya, B. P. and Patra, K., On metabelian groups of automorphisms of compact Riemann surfaces, J. London Math. Soc. 33 (1986), 467–472.CrossRefGoogle Scholar
3.Greenleaf, N. and May, C. L., Bordered Klein surfaces with maximal symmetry. Trans. Amer. Math. Soc. 274 (1982) 265–283.CrossRefGoogle Scholar
4.Harvey, W. J., Cyclic groups of automorphisms of a compact Riemann surface, Quart. J. Math. Oxford Ser. 2 17 (1966), 86–98.CrossRefGoogle Scholar
5.Hurwitz, A., Uber algebraische Gebilde mit eindeutigen Transformationen in sich, Math. Ann. 41 (1893), 403–442.CrossRefGoogle Scholar
6.Lehner, J. and Newman, M., On Riemann surfaces with maximal automorphism groups, Glasgow Math. J. 8 (1967), 102–112.CrossRefGoogle Scholar
7.Macbeath, A. M., On a theorem of Hurwitz, Proc. Glasgow Math. Assoc., 5 (1961), 90–96.CrossRefGoogle Scholar
8.Macbeath, A. M., Generators of the linear fractional groups, Proc. Symp. Pure Math. Vol. XII, Amer. Math. Soc. (1969), 14–32.Google Scholar
9.Macbeath, A. M., Discontinuous groups and birational transformations, Proc. Dundee Summer School 1961.Google Scholar
10.Maclachlan, C., Abelian groups of automorphisms of compact Riemann surfaces, Proc. London Math. Soc. (3) 15 (1965), 699–712.CrossRefGoogle Scholar
11.May, C. L., Supersoluble M*-groups, Glasgow Math. J. 30 (1988), 31–40.CrossRefGoogle Scholar
12.Robinson, D. J. S., A course in the Theory of Groups (Springer Verlag, 1982).CrossRefGoogle Scholar
13.Singerman, D., Automorphisms of compact non-orientable Riemann surfaces, Glasgow Math. J., 12 (1971), 50–59.CrossRefGoogle Scholar
14.Singerman, D., Subgroups of Fuchsian groups and finite permutation groups. Bull. London Math. Soc. 2 (1970), 319–323.CrossRefGoogle Scholar
15.Zomorrodian, R., Nilpotent automorphism groups of Riemann surfaces, Trans. Amer. Math. Soc. 288 (1985), 241–255.Google Scholar
16.Zomorrodian, R., Classification of p-groups of automorphisms of Riemann surfaces and their lower series, Glasgow Math. J. 29 (1987), 237–244.CrossRefGoogle Scholar