Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mattila, Kirsti
1980.
On normal and compact operators on Banach spaces.
Israel Journal of Mathematics,
Vol. 37,
Issue. 1-2,
p.
164.
Campbell, S. L.
and
Faulkner, G. D.
1980.
Operators on Banach spaces with complemented ranges.
Acta Mathematica Academiae Scientiarum Hungaricae,
Vol. 35,
Issue. 1-2,
p.
123.

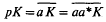 and (1 –
and (1 – 