No CrossRef data available.
Article contents
Sur une question de localisation
Published online by Cambridge University Press: 18 May 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
II est connu [4] que si A = U(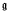 ) est l'algèbre enveloppante d'une algèbre de Lie nilpotente
) est l'algèbre enveloppante d'une algèbre de Lie nilpotente 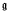 de dimension finie sur un corps F de caractéristique 0, tout idéal (complètement) premier P a pourlocalisé R = Ap un anneau régulier au sens de [5]; c'est-à-dire que le radical de Jacobson
de dimension finie sur un corps F de caractéristique 0, tout idéal (complètement) premier P a pourlocalisé R = Ap un anneau régulier au sens de [5]; c'est-à-dire que le radical de Jacobson 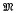 de R est engendrè par une suite centralisante régulière de longueur n = K-dim R, soit (z1…, zn). Dans le cas très particulier où P est l'idéal d'augmentation de U(
de R est engendrè par une suite centralisante régulière de longueur n = K-dim R, soit (z1…, zn). Dans le cas très particulier où P est l'idéal d'augmentation de U(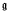 ) il suffit de prendre pour (z1…, zn) l'image dans U(
) il suffit de prendre pour (z1…, zn) l'image dans U(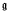 )p d'une base de
)p d'une base de 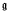 sur F adaptée à la suite centrale ascendante de
sur F adaptée à la suite centrale ascendante de 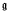 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1981
References
BIBLIOGRAPHIE
3.Malliavin, M. P., Régularité locale d'algèbres universelles. C. R. Acad. Sc. Paris t. 283 (1976), 923–925.Google Scholar
4.Smith, P. F., On non commutative regular rings, Glasgow Math. J. 17 (1976), 98–102.CrossRefGoogle Scholar
5.Walker, R., Local rings and normalizing sets of elements, Proc. London Math. Soc. (3) 24 (1972), 27–45.Google Scholar

