Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Glover, Keith
and
Partington, Jonathan R.
1987.
Modelling, Robustness and Sensitivity Reduction in Control Systems.
p.
95.
Glover, K.
Lam, J.
and
Partington, J. R.
1991.
Rational approximation of a class of infinite-dimensional systems II: Optimal convergence rates ofL ∞ approximants.
Mathematics of Control, Signals, and Systems,
Vol. 4,
Issue. 3,
p.
233.
Das, Namita
and
Partington, Jonathan R.
1994.
Little Hankel operators on the half plane.
Integral Equations and Operator Theory,
Vol. 20,
Issue. 3,
p.
306.
2002.
Geometric Function Theory.
Vol. 1,
Issue. ,
p.
75.
Vitse, Pascale
2005.
Functional calculus under Kreiss type conditions.
Mathematische Nachrichten,
Vol. 278,
Issue. 15,
p.
1811.
Shah, Parikshit
Bhaskar, Badri Narayan
Tang, Gongguo
and
Recht, Benjamin
2012.
Linear system identification via atomic norm regularization.
p.
6265.
Queffélec, H.
and
Zarouf, R.
2019.
On Bernstein’s inequality for polynomials.
Analysis and Mathematical Physics,
Vol. 9,
Issue. 3,
p.
1181.
Charpentier, Stéphane
Fouchet, Karine
and
Zarouf, Rachid
2023.
On the condition number of a Kreiss matrix.
Canadian Mathematical Bulletin,
Vol. 66,
Issue. 4,
p.
1376.

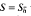 with
with 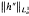 cannot give an estimate for
cannot give an estimate for 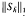 since the first two terms in the coefficient sequence of the Hankel operator have been removed by differentiation.
since the first two terms in the coefficient sequence of the Hankel operator have been removed by differentiation.