Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-15T10:01:00.289Z Has data issue: false hasContentIssue false
  • English
  • Français

Symmetries of surfaces: an extension of Kulkarni's theorem

Published online by Cambridge University Press:  18 May 2009

Gareth A. Jones
Gareth A. Jones
Affiliation:
Department of Mathematics, University of Southampton, Southampton SO9 5NH, England
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [6] Kulkarni considered the set of values of g for which a given finite group G acts faithfully as a group of orientation-preserving self-homeomorphisms of a compact, connected, orientable surface σg of genus g. Let us denote this set by 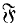(G). Then Kulkarni showed that there exists a positive integer Kdepending only on the order d = |G| of G, the exponent e= exp G of G and the structure of a Sylow 2-subgroup G2 of G, satisfying:

Theorem 1. (Kulkarni [6]) 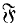(G) consists of all but finitely many non-negative integers g ≡ 1 mod K.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 36 , Issue 2 , May 1994 , pp. 173 - 184
Copyright
Copyright © Glasgow Mathematical Journal Trust 1994

References

REFERENCES

1.Aschbacher, M. and Guralnick, R., Some applications of the first cohomology group, J. Algebra, 90 (1984), 446–460.CrossRefGoogle Scholar
2.Martino, L. Di and Tamburini, M. C., 2-generation of finite simple groups and some related topics, in Generators and Relations in Groups and Geometries (ed. Barlotti, A. et al. ), (Kluwer, 1991).Google Scholar
3.Guralnick, R. M. and Thompson, J. G., Finite groups of genus zero, J. Algebra, 131 (1990), 303–341.CrossRefGoogle Scholar
4.Hurwitz, A., Über algebraische Gebilde mit eindeutigen Transformationenin sich. Math. Ann., 41 (1893), 403–442.CrossRefGoogle Scholar
5.Kuiken, K., On the monodromy groups of Riemann surfaces of genus zero, J. Algebra, 59 (1979), 481–489.CrossRefGoogle Scholar
6.Kulkarni, R. S., Symmetries of surfaces, Topology, 26 (1987), 195–203.CrossRefGoogle Scholar
7.Kulkarni, R. S. and Maclachlan, C., Cyclic p-groups of symmetries of surfaces, Glasgow Math.J., 33 (1991), 213–221.CrossRefGoogle Scholar
8.Liebeck, M. and Saxl, J., Minimal degrees of primitive permutation groups, with an application to monodromy groups of covers of Riemann surfaces Proc. London Math. Soc., (3)63 (1991), 266–315.CrossRefGoogle Scholar
9.Miller, G. A., On the groups generated by two operators, Bull. Amer. Math. Soc., 7 (1901), 424–426.CrossRefGoogle Scholar
10.Serre, J-P., Groupes de Galois sur , Astérisque, 161–162 (1988), 73–85.Google Scholar
11.Steinberg, R., Generators for simple groups, Canad. J. Math., 14 (1962), 277–283.CrossRefGoogle Scholar